定理介紹
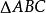 外角平分線定理
外角平分線定理 外角平分線定理
外角平分線定理 外角平分線定理
外角平分線定理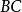 外角平分線定理
外角平分線定理 外角平分線定理
外角平分線定理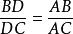 外角平分線定理
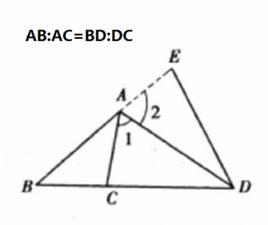
外角平分線定理三角形外角平分線定理:三角形外角的平分線如果和對邊的延長線相交,它按照夾相應角的兩邊的比外分對邊。如下圖,在中,外角的平分線交的延長線於,則。
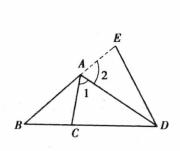 圖1
圖1定理的證明
證法一
如圖1,在BA的延長線上任取一點E,連線DE
 外角平分線定理
外角平分線定理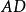 外角平分線定理
外角平分線定理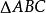 外角平分線定理
外角平分線定理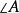 外角平分線定理
外角平分線定理是中的外角平分線,
 外角平分線定理
外角平分線定理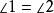 外角平分線定理
外角平分線定理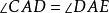 外角平分線定理
外角平分線定理即,
 外角平分線定理
外角平分線定理由三角形等角定理得:
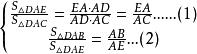 外角平分線定理
外角平分線定理 外角平分線定理
外角平分線定理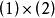 外角平分線定理
外角平分線定理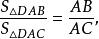 外角平分線定理
外角平分線定理得:
 外角平分線定理
外角平分線定理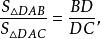 外角平分線定理
外角平分線定理又
 外角平分線定理
外角平分線定理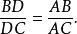 外角平分線定理
外角平分線定理證法二
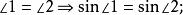 外角平分線定理
外角平分線定理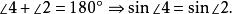 外角平分線定理
外角平分線定理由正弦定理,得:
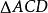 外角平分線定理
外角平分線定理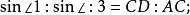 外角平分線定理
外角平分線定理中,
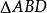 外角平分線定理
外角平分線定理 外角平分線定理
外角平分線定理中,
 外角平分線定理
外角平分線定理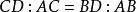 外角平分線定理
外角平分線定理,
 外角平分線定理
外角平分線定理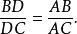 外角平分線定理
外角平分線定理三角形外角平分線逆定理
 外角平分線定理
外角平分線定理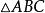 外角平分線定理
外角平分線定理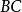 外角平分線定理
外角平分線定理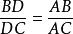 外角平分線定理
外角平分線定理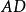 外角平分線定理
外角平分線定理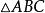 外角平分線定理
外角平分線定理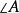 外角平分線定理
外角平分線定理如圖1,若是的邊延長線上的一個點,且滿足,則是的的外角平分線。
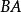 外角平分線定理
外角平分線定理 外角平分線定理
外角平分線定理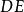 外角平分線定理
外角平分線定理證明:如圖1,在的延長線上任取一點,連線。
 外角平分線定理
外角平分線定理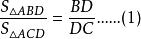 外角平分線定理
外角平分線定理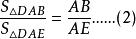 外角平分線定理
外角平分線定理 外角平分線定理
外角平分線定理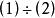 外角平分線定理
外角平分線定理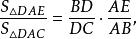 外角平分線定理
外角平分線定理得
 外角平分線定理
外角平分線定理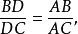 外角平分線定理
外角平分線定理 外角平分線定理
外角平分線定理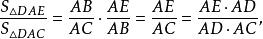 外角平分線定理
外角平分線定理 外角平分線定理
外角平分線定理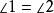 外角平分線定理
外角平分線定理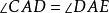 外角平分線定理
外角平分線定理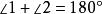 外角平分線定理
外角平分線定理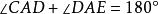 外角平分線定理
外角平分線定理由三角形等角逆定理得:,即或,即,
 外角平分線定理
外角平分線定理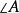 外角平分線定理
外角平分線定理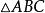 外角平分線定理
外角平分線定理是的外角,
 外角平分線定理
外角平分線定理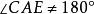 外角平分線定理
外角平分線定理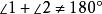 外角平分線定理
外角平分線定理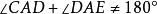 外角平分線定理
外角平分線定理,即,也就是,
 外角平分線定理
外角平分線定理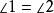 外角平分線定理
外角平分線定理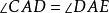 外角平分線定理
外角平分線定理,即,
 外角平分線定理
外角平分線定理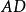 外角平分線定理
外角平分線定理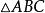 外角平分線定理
外角平分線定理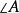 外角平分線定理
外角平分線定理是的的外角平分線。