三角形內角平分線定理

三角形內角平分線定理：三角形任意兩邊之比等於它們夾角的平分線分對邊之比。

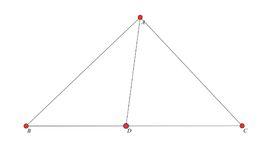
三角形內角平分線定理

三角形內角平分線性質定理：在ΔABC中,若AD是∠A的平分線,則BD/DC=AB/AC

套用：不用計算即可將一條線段按要求分成任意比例

三角形內角平分線內分對邊，所得的兩條線段與這個角的兩邊對應成比例.

三角形外角平分線的性質定理：三角形外角平分線外分對邊，所得的兩條線段與其內角的兩邊對應成比例.

證明方法

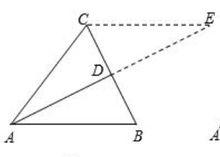三角形內角平分線定理

可用相似三角形證明：如下圖，過點C作CE平行AB交AD延長線於E，則有三角形ABD相似於三角形ECD，故AB/CE=BD/CD，易由平分線證出AC=CE，所以AB/AC=BD/CD，結論得證.

也可通過三角函式證明：三角形ACD面積=1/2*AC*AD*sinCAD；三角形BAD面積=1/2*AB*AD*sinBAD，又有兩個三角形面積比等於CD/BD，故結論得證.

外角平分線性質定理可用面積法以及角平分線定理推導.

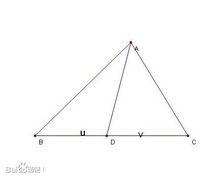三角形內角平分線定理的證明