性質介紹
設⊿ABC的角A、B、C的對邊分別為a、b、c,p=(a+b+c)/2.
1、三角形的外角平分線都在三角形外。
2、三角形的一條內角的平分線與不相鄰的兩個外角的平分線交於一點,該點叫做三角形的旁心。
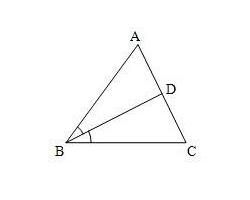
3、三角形角平分線有個有趣的性質:三角形ABC中角A的平分線為AD,則AB:AC=BD:CD。(可用面積法證明)
4、三角形的角平分線都在三角形內。
 三角形角平分線
三角形角平分線5、設三角形ABC,∠A平分線AD,AB=c,AC=b,BC=a,半周長p=(a+b+c)/2,
三條角平分線為ta,tb,tc,AD=ta,BE=tb,CF=tc,
根據角平分線性質,BD/CD=c/b,(角平分對邊二部分之比為其鄰邊之比),
(b+c)/b=(BD+CD)/CD=a/CD,(合比)
CD=ab/(b+c),
在△ADC中,根據餘弦定理,
AD^2=b^2+CD^2-2CD*b*cosC
=b^2+a^2b^2/(b+c)^2-2ab^2*cosC/(b+c),
根據餘弦定理,cosC=(a^2+b^2-c^2)/(2ab),
AD^2= b^2+a^2b^2/(b+c)^2-b(a^2+b^2-c^2)/(b+c)
AD^2=bc[(b+c)^2-a^2]/(b+c)^2=bc[(b+c-a)(b+c+a)]/(b+c)^2,
Ta=AD=√[(bc*2p*(2p-2a))/(b+c)
=[2/(b+c)]√[bcp(p-a)].
同理可證,tb=[2/(a+c)]√[acp(p-b)].
tc=[2/(a+b)]√[abp(p-c)].
6、三角形的三條角平分線交於一點,該點叫做三角形的內心。常記作點I。