圓的方程
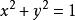圓的標準方程所表示的曲線是以O(0，0)為圓心，以1單位長度為半徑的圓；
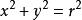圓的標準方程所表示的曲線是以O(0，0)為圓心，以r為半徑的圓；
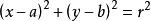圓的標準方程所表示的曲線是以O(a，b)為圓心，以r為半徑的圓。
確定圓的方程主要方法是待定係數法，即列出關於a、b、r的方程組，求a、b、r，或直接求出圓心(a，b)和半徑r，一般步驟為：
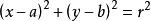圓的標準方程根據題意，設所求的圓的標準方程；
根據已知條件，建立關於a、b、r的方程組；
解方程組，求出a、b、r的值，並把它們代入所設的方程中去，就得到所求圓的方程。
方程推導
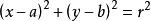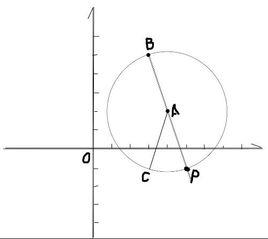
圓的標準方程在平面直角坐標系中，設有圓O，圓心O(a,b) 點P(x,y)是圓上任意一點。
圓是平面到定點距離等於定長的所有點的集合。
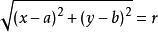圓的標準方程所以。
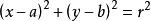圓的標準方程兩邊平方，得到。
點與圓
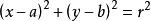圓的標準方程點P（x,y) 與圓 的位置關係：
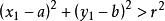圓的標準方程⑴當 時，則點P在圓外。
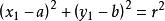圓的標準方程⑵當 時，則點P在圓上。
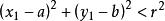圓的標準方程⑶當 時，則點P在圓內。
直線與圓
位置關係
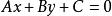圓的標準方程
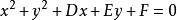圓的標準方程平面內，直線 與圓 的位置關係判斷一般方法是：
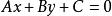圓的標準方程
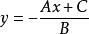圓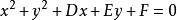的標準方程 圓的標準方程
圓的標準方程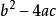
圓的標準方程1.由 ，可得 ，（其中B不等於0），代入 ，即成為一個關於x的一元二次方程 。利用判別式 的符號可確定圓與直線的位置關係如下：
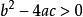圓的標準方程如果 ，則圓與直線有2交點，即圓與直線相交。
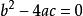圓的標準方程如果 ，則圓與直線有1交點，即圓與直線相切。
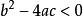圓的標準方程如果 ，則圓與直線有0交點，即圓與直線相離。
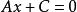圓的標準方程
圓的標準方程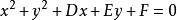 圓的標準方程 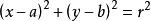圓的標準方程
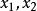圓的標準方程
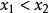圓的標準方程2.如果B=0即直線為 ，即 ，它平行於y軸（或垂直於x軸），將 化為 。令y=b，求出此時的兩個x值，並且規定 ，那么：
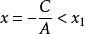圓的標準方程
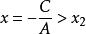圓的標準方程當 或 時，直線與圓相離；
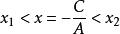圓的標準方程當 時，直線與圓相交；
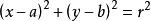圓的標準方程在直角坐標系中，圓的標準方程為： ;
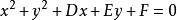圓的標準方程
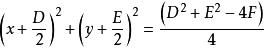圓的標準方程
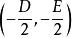圓的標準方程=> => 圓心坐標為
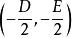圓的標準方程 圓的標準方程其實只要保證前係數都是1,就可以直接判斷出圓心坐標為,這可以作為一個結論運用,
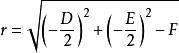圓的標準方程且
圓上一點的切線方程：
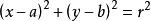圓的標準方程
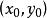圓的標準方程
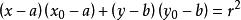圓的標準方程上任意一點該點的切線方程：。
如果在平面直角坐標系中還可以直接將直線方程與圓的方程聯立得出：
若△>0 則該方程有兩個根，即直線與圓有兩個交點，相交；
若△=0 則該方程有一個根，即直線與圓有一個交點，相切；
若△<0 則該方程有零個根，即直線與圓有零個交點，相離。
代數法
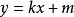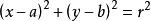圓的標準方程 圓的標準方程
圓的標準方程如果直線方程，圓的方程為 ,將直線方程代入圓的方程，消去y，得關於x的一元二次方程,那么：
a.當△<0時，直線與圓沒有公共點；
b.當△=0時，直線與圓相切；
c.當△>0時，直線與圓相交。
幾何法
求出圓心到直線的距離d，半徑為r：
d>r，則直線與圓相離；
d=r，則直線與圓相切；
d<r，則直線與圓相交。
兩圓位置關係
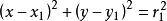圓的標準方程
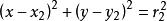圓的標準方程若兩圓的方程分別為C： ，C₂： ：
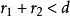圓的標準方程則兩圓外離 ；
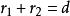圓的標準方程兩圓外切 ；
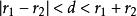圓的標準方程兩圓相交 ；
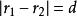圓的標準方程兩圓內切 ；
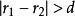圓的標準方程兩圓內含 .
一般式
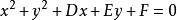圓的標準方程此方程可用於解決兩圓的位置關係：
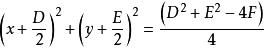圓的標準方程配方化為標準方程：，
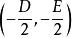圓的標準方程其圓心坐標：，
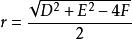圓的標準方程半徑為，
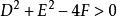圓的標準方程此方程滿足為圓的方程的條件是:。
若不滿足,則不可表示為圓的方程。
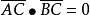圓的標準方程
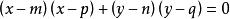圓的標準方程已知直徑的兩個端點坐標A(m，n)、B(p，q)設圓上任意一點C(x，y)。則有：； 可推出方程：再整理即可得出一般方程。
