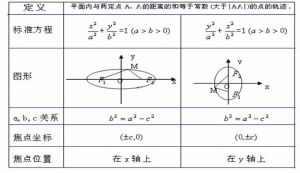
橢圓的標準方程

橢圓的標準方程共分兩種情況：當焦點在x軸時，橢圓的標準方程是：x^2/a^2+y^2/b^2=1，(a>b>0)；當焦點在y軸時，橢圓的標準方程是：y^2/a^2+x^2/b^2=1，(a>b>0)；其中a^2-c^2=b^2。

基本信息

• 中文名：橢圓標準方程
• 其他外文名：Standard equation of the ellipse

• 別稱：線條
• 表達式：x^2/a^2+y^2/b^2=1
• 提出者：數學家
• 提出時間：19世紀
• 套用學科：數學
• 適用領域範圍：數學幾何，解析幾何

方程推導

橢圓的標準方程

設橢圓的兩個焦點分別為F1，F2，它們之間的距離為2c，橢圓上任意一點到F1，F2的距離和為2a（2a>2c）。
以F1，F2所在直線為x軸，線段F1F2的垂直平分線為y軸，建立直角坐標系xOy，則F1,F2的坐標分別為（-c,0)，（c,0)。

非標準方程

其方程是二元二次方程，可以利用二元二次方程的性質進行計算，分析其特性。

幾何性質

X，Y的範圍
當焦點在X軸時-a≤x≤a,-b≤y≤b
當焦點在Y軸時-b≤x≤b,-a≤y≤a
對稱性
不論焦點在X軸還是Y軸，橢圓始終關於X/Y/原點對稱。
頂點：
焦點在X軸時：長軸頂點：（-a，0），（a，0）
短軸頂點：（0，b），（0，-b）
焦點在Y軸時：長軸頂點：（0,-a），（0,a）
短軸頂點：（b,0），（-b,0）
注意長短軸分別代表哪一條軸，在此容易引起混亂，還需數形結合逐步理解透徹。
焦點：
當焦點在X軸上時焦點坐標F1（-c,0）F2(c,0)
當焦點在Y軸上時焦點坐標F1（0，-c）F2(0,c)

計算方法

(（其中分別是橢圓的長半軸、短半軸的長，可由圓的面積可推導出來)或（其中分別是橢圓的長軸，短軸的長）。
圓和橢圓之間的關係：
橢圓包括圓，圓是特殊的橢圓。