定義
 有序對
有序對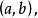 有序對
有序對 有序對
有序對由兩個元素和b按一定的順序排列成的二元組叫做 有序對(或 有序偶),記作其中稱為 第一元素,b稱為 第二元素 。
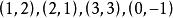 有序對
有序對有序對可以表示有一定次序關係成對出現的事物,如平面直角坐標系中點的坐標就是有序對,都代表平面直角坐標系中不同的點。在有序對中兩個元素的次序是十分重要的。
有序對的特點
一般說來有序對具有以下特點:
1)當a≠b時,(a,b)和(b,a)是兩個不同的有序對。
2)兩個有序對相等,即(a,b)=(c,d)的充分必要條件是a=c且b=d。
注意,(a,b)和(b,a)是不同的。除非a=b,否則(a,b)和(b,a)是不等的。但是集合(a,b}和集合{b,a)是相等的,即{a,b}一{b,a},因為集合中的元素是無順序的 。
【 例1】證明<x,y>=<u,v>的充分必要條件是x=u且y=v。
證明: 充分性 顯然成立。
必要性 若<x,y>=<u,v>,則
{x}∈{{x},{x,y}}=<x,y>=<u,v>= {{u},{u,v}}.
(1) 若{x}={u},則因為u∈{u}={x},所以u=x。
(2) 若{x}={u,v},則因為u∈{u,v}={x},所以有u=x,{u}={x}。故總有{x}={u}及x=u成立。
由{{x},{x,y}}={{u},{u,v}},{x}={u}得{x,y}= {u,u}。再由{x,y}={u,v}和x=u可得y=v。
在實際問題中有時會用到有序3元組,有序4元組,....,有序n 元組。可以用有序對來定義有序n元組 。
有序n元組
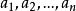 有序對
有序對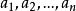 有序對
有序對 有序對
有序對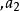 有序對
有序對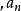 有序對
有序對由n個元素,按一定的順序排列成的一個序列(),稱為 有序n元組,其中為第一元素為第二個素,…為第n元素 。
例如,n維空間中點的坐標或n維向量都是有序n元組,(1,2,5)、(-1,-2,3)等是三維空間直角坐標系中點的坐標。
若且唯若兩個有序n元組的每一對對應的元素都相等時,它們才相等。也就是說
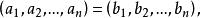 有序對
有序對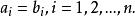 有序對
有序對當且僅

