基礎定義
一般地,對於函式f(x)
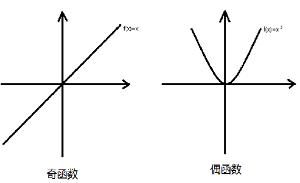
⑴如果對於函式f(x)定義域內的任意一個x,都有f(x)=f(-x)或f(x)/f(-x)=1那么函式f(x)就叫做偶函式。關於y軸對稱,f(-x)=f(x)。
⑵如果對於函式f(x)定義域內的任意一個x,都有f(-x)=-f(x)或f(x)/f(-x)=-1,那么函式f(x)就叫做奇函式。關於原點對稱,-f(x)=f(-x)。
⑶如果對於函式定義域內的任意一個x,都有f(x)=f(-x)和f(-x)=-f(x),(x∈R,且R關於原點對稱.)那么函式f(x)既是奇函式又是偶函式,稱為既奇又偶函式。
⑷如果對於函式定義域內的存在一個a,使得f(a)≠f(-a),存在一個b,使得f(-b)≠-f(b),那么函式f(x)既不是奇函式又不是偶函式,稱為非奇非偶函式。
定義域互為相反數,定義域必須關於原點對稱
特殊的,f(x)=0既是奇函式,又是偶函式。
說明:①奇、偶性是函式的整體性質,對整個定義域而言。
②奇、偶函式的定義域一定關於原點對稱,如果一個函式的定義域不關於原點對稱,則這個函式一定不具有奇偶性。
(分析:判斷函式的奇偶性,首先是檢驗其定義域是否關於原點對稱,然後再嚴格按照奇、偶性的定義經過化簡、整理、再與f(x)比較得出結論)
③判斷或證明函式是否具有奇偶性的根據是定義。
④如果一個奇函式f(x)在x=0處有意義,則這個函式在x=0處的函式值一定為0。並且關於原點對稱。
⑤如果函式定義域不關於原點對稱或不符合奇函式、偶函式的條件則叫做非奇非偶函式。例如f(x)=x³【-∞,-2】或【0,+∞】(定義域不關於原點對稱)
⑥如果函式既符合奇函式又符合偶函式,則叫做既奇又偶函式。例如f(x)=0
註:任意常函式(定義域關於原點對稱)均為偶函式,只有f(x)=0是既奇又偶函式