性質
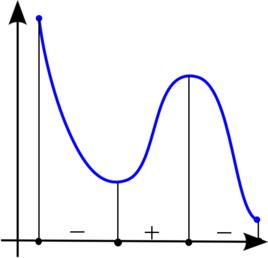
若函式y=f(x)在某個區間是增函式或減函式,則就說函式在這一區間具有(嚴格的)單調性,這一區間叫做函式的單調區間。此時也說函式是這一區間上的單調函式。
註:在單調性中有如下性質。圖例:↑(增函式)↓(減函式)
↑+↑=↑ 兩個增函式之和仍為增函式
↑-↓=↑ 增函式減去減函式為增函式
↓+↓=↓ 兩個減函式之和仍為減函式
↓-↑=↓ 減函式減去增函式為減函式
一般地,設函式f(x)的定義域為I:
如果對於屬於I內某個區間上的任意兩個自變數的值x1、x2,當x1<x2時都有f(x1)<f(x2)。那么就說f(x)在這個區間上是增函式。
相反地,如果對於屬於I內某個區間上的任意兩個自變數的值x1、x2,當x1<x2時都有f(x1)>f(x2),那么f(x)在這個區間上是減函式。
例題
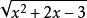 單調區間
單調區間y=
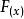 單調區間
單調區間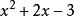 單調區間
單調區間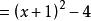 單調區間
單調區間【解】設=
其函式圖象的對稱軸是x=-1,
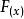 單調區間
單調區間∴當x<-1時,是單調遞減函式。
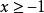 單調區間
單調區間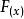 單調區間
單調區間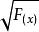 單調區間
單調區間當時,是單調遞增函式y== ,
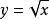 單調區間
單調區間(此處y是一個複合函式,它的外層函式是,是一個單調遞增函式)
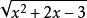 單調區間
單調區間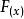 單調區間
單調區間∴y=的單調性由裡層函式決定。
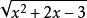 單調區間
單調區間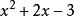 單調區間
單調區間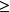 單調區間
單調區間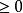 單調區間
單調區間又∵y=的定義域是(x+3)(x-1),
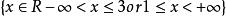 單調區間
單調區間解得。
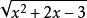 單調區間
單調區間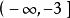 單調區間
單調區間∴當x<=-3時,y是單調遞減函式;x>=1時,y是單調遞增函式y=的單調減區間是,單調增區間是[1,+∞) 。