定義
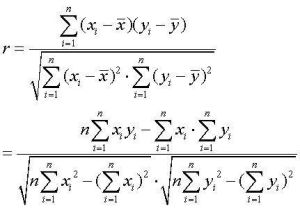相關係數公式簡單相關係數：又叫相關係數或線性相關係數，一般用字母r表示，用來度量兩個變數間的線性關係。
復相關係數：又叫多重相關係數。復相關是指因變數與多個自變數之間的相關關係。例如，某種商品的季節性需求量與其價格水平、職工收入水平等現象之間呈現復相關關係。
典型相關係數：是先對原來各組變數進行主成分分析，得到新的線性關係的綜合指標，再通過綜合指標之間的線性相關係數來研究原各組變數間相關關係。
性質
(1)定理：|ρXY|=1的充要條件是，存在常數a，b，使得P{Y=a+bX}=1；相關係數ρXY取值在-1到1之間，ρXY=0時，稱X,Y不相關；|ρXY|=1時，稱X,Y完全相關，此時，X,Y之間具有線性函式關係；|ρXY|<1時，X的變動引起Y的部分變動，ρXY的絕對值越大，X的變動引起Y的變動就越大，|ρXY|>0.8時稱為高度相關，當|ρXY|<0.3時稱為低度相關，其它時候為中度相關。
(2)推論：若Y=a+bX，則有
證明：令E(X)=μ，D(X)=σ2
則E(Y)=bμ+a，D(Y)=b2σ2
E(XY)=E(aX+bX2)=aμ+b(σ2+μ2)
Cov(X,Y)=E(XY)−E(X)E(Y)=bσ2
若b≠0，則ρXY≠0。
若b=0，則ρXY=0。
軟體公司在全國有許多代理商，為研究它的財務軟體產品的廣告投入與銷售額的關係，統計人員隨機選擇10家代理商進行觀察，蒐集到年廣告投入費和月平均銷售額的數據，並編製成相關表，見表1:
表1廣告費與月平均銷售額相關表，單位：萬元
| 年廣告費投入 | 月均銷售額 |
|---|---|
| 12.5 15.3 23.2 26.4 33.5 34.4 39.4 45.2 55.4 60.9 | 21.2 23.9 32.9 34.1 42.5 43.2 49.0 52.8 59.4 63.5 |
| 序號 | 廣告投入(萬元) x | 月均銷售額(萬元) y |  |  |  |
|---|---|---|---|---|---|
| 1 2 3 4 5 6 7 8 9 10 | 12.5 15.3 23.2 26.4 33.5 34.4 39.4 45.2 55.4 60.9 | 21.2 23.9 32.9 34.1 42.5 43.2 49.0 52.8 59.4 63.5 | 156.25 234.09 538.24 696.96 1122.25 1183.36 1552.36 2043.04 3069.16 3708.81 | 449.44 571.21 1082.41 1162.81 1806.25 1866.24 2401.00 2787.84 3528.36 4032.25 | 265.00 365.67 763.28 900.24 1423.75 1486.08 1930.60 2386.56 3290.76 3867.15 |
| 合計 | 346.2 | 422.5 | 14304.52 | 19687.81 | 16679.09 |
相關係數為0.9942，說明廣告投入費與月平均銷售額之間有高度的線性正相關關係。
套用
1.在機率論計算中的套用
相關係數解：由於X+Y=n，則Y=-X+n，根據相關係數的性質推論，得ρXY=−1。
例2．已知隨機變數X、Y分別服從常態分配N(1，9)，N(0，16)且X，Y的相關係數
設，求證X，Z相互獨立。
證明：由已知得E(X)=1，D(X)=9，E(Y)=0，D(Y)=16
由於常態分配的隨機變數的線性組合仍然服從常態分配，知Z是正態變數。
根據數學期望的性質有
根據方差的性質有得
由於E(XY)=Cov(X,Y)+E(X)E(Y)=−6，
E(X)=D(X)+[E(X)]=10
ρXZ=0，X，Z不相關。
由於正態隨機變數的相互獨立與互不相關等價，故X,Z相互獨立。
因此，一般情況下兩個隨機變數不相關不一定相互獨立。不相關僅指隨機變數之間沒有線性關係，而相互獨立則表明隨機變數之間互不影響，沒有關係。
2.在企業物流上的套用
【例】一種新產品上市。在上市之前，公司的物流部需把新產品合理分配到全國的10個倉庫，新品上市一個月後，要評估實際分配方案與之前考慮的其他分配方案中，是實際分配方案好還是其中尚未使用的分配方案更好，通過這樣的評估，可以在下一次的新產品上市使用更準確的產品分配方案，以避免由於分配而產生的積壓和斷貨。表1是根據實際數據所列的數表。
通過計算，很容易得出這3個分配方案中，B的相關係數是最大的，這樣就評估到B的分配方案比實際分配方案A更好，在下一次的新產品上市分配計畫中，就可以考慮用B這種分配方法來計算實際分配方案。
3.在聚類分析中的套用
【例】如果有若干個樣品，每個樣品有n個特徵，則相關係數可以表示兩個樣品間的相似程度。藉此，可以對樣品的親疏遠近進行距離聚類。例如9個小麥品種(分別用A1,A2,...,A9表示)的6個性狀，作相關係數計算並檢驗。
由相關係數計算公式可計算出6個性狀間的相關係數，分析及檢驗結果見表3。由表3可以看出，冬季分櫱與每穗粒數之間呈現負相關(ρ=−0.8982)，即麥冬季分櫱越多，那么每穗的小麥粒數越少，其他性狀之間的關係不顯著。
缺點
需要指出的是，相關係數有一個明顯的缺點，即它接近於1的程度與數據組數n相關，這容易給人一種假象。因為，當n較小時，相關係數的波動較大，對有些樣本相關係數的絕對值易接近於1；當n較大時，相關係數的絕對值容易偏小。特別是當n=2時，相關係數的絕對值總為1。因此在樣本容量n較小時，我們僅憑相關係數較大就判定變數x與y之間有密切的線性關係是不妥當的。
例如，就我國深滬兩股市資產負債率與每股收益之間的相關關係做研究。發現1999年資產負債率前40名的上市公司，二者的相關係數為r=–0.6139；資產負債率後20名的上市公司，二者的相關係數r=0.1072；而對於滬、深全部上市公司（基金除外）結果卻是，r滬=–0.5509，r深=–0.4361，根據三級劃分方法，兩變數為顯著性相關。這也說明僅憑r的計算值大小判斷相關程度有一定的缺陷。
