定義
 嚴格單調函式
嚴格單調函式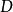 嚴格單調函式
嚴格單調函式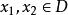 嚴格單調函式
嚴格單調函式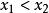 嚴格單調函式
嚴格單調函式設 為定義在 上的函式.。 若對於任何 ,當 時,總有
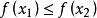 嚴格單調函式
嚴格單調函式 嚴格單調函式
嚴格單調函式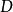 嚴格單調函式
嚴格單調函式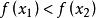 嚴格單調函式
嚴格單調函式 嚴格單調函式
嚴格單調函式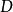 嚴格單調函式
嚴格單調函式(i) ,則稱 為 上的增函式,特別當成立嚴格不等式 時,稱 為 上的嚴格增函式;
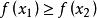 嚴格單調函式
嚴格單調函式 嚴格單調函式
嚴格單調函式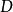 嚴格單調函式
嚴格單調函式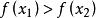 嚴格單調函式
嚴格單調函式 嚴格單調函式
嚴格單調函式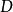 嚴格單調函式
嚴格單調函式(ii) ,則稱 為 上的減函式,特別當成立嚴格不等式 時,稱 為 上的嚴格減函式;
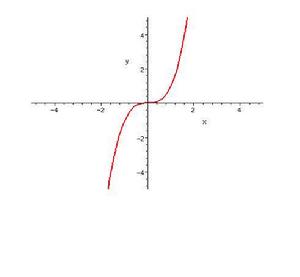
增函式和減函式統稱為單調函式,嚴格增函式和嚴格減函式統稱為 嚴格單調函式。
性質
 嚴格單調函式
嚴格單調函式嚴格單調函式的圖像與任意平行於 軸的直線至多有一個交點,這一特性保證了它必定具有反函式。
定理
定理 1
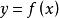 嚴格單調函式
嚴格單調函式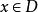 嚴格單調函式
嚴格單調函式 嚴格單調函式
嚴格單調函式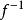 嚴格單調函式
嚴格單調函式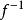 嚴格單調函式
嚴格單調函式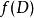 嚴格單調函式
嚴格單調函式設 , 為嚴格增(減)函式,則 必有反函式 ,且 在其定義域 上也是嚴格增(減)函式。
定理 2
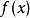 嚴格單調函式
嚴格單調函式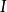 嚴格單調函式
嚴格單調函式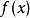 嚴格單調函式
嚴格單調函式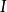 嚴格單調函式
嚴格單調函式設 在區間 上可導,則 在 上遞增(減)的充要條件是
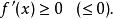 嚴格單調函式
嚴格單調函式定理 3
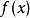 嚴格單調函式
嚴格單調函式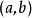 嚴格單調函式
嚴格單調函式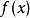 嚴格單調函式
嚴格單調函式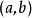 嚴格單調函式
嚴格單調函式若函式 在 上可導,則 在 上嚴格遞增(遞減)的充要條件是:
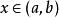 嚴格單調函式
嚴格單調函式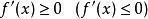 嚴格單調函式
嚴格單調函式(i)對一切 ,有 ;
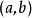 嚴格單調函式
嚴格單調函式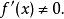 嚴格單調函式
嚴格單調函式(ii)在 的任何子區間上
推論 1
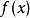 嚴格單調函式
嚴格單調函式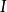 嚴格單調函式
嚴格單調函式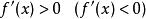 嚴格單調函式
嚴格單調函式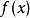 嚴格單調函式
嚴格單調函式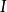 嚴格單調函式
嚴格單調函式設函式 在區間 上可微,若 ,則 在 上嚴格遞增(嚴格遞減)。
注
 嚴格單調函式
嚴格單調函式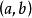 嚴格單調函式
嚴格單調函式 嚴格單調函式
嚴格單調函式 嚴格單調函式
嚴格單調函式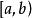 嚴格單調函式
嚴格單調函式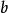 嚴格單調函式
嚴格單調函式若 在 上(嚴格)遞增(減),且在點 右連續,則 在 上亦為(嚴格)遞增(減),對右端點 可類似討論。