舉例
例如,定義在實數上的函式f,
f(x)=x -3x+4,
則2是函式f的一個不動點,因為 f(2)=2。
也不是每一個函式都具有不動點。例如定義在實數上的函式f(x)=x+1就沒有不動點。因為對於任意的實數,x永遠不會等於x+1。用畫圖的話來說,不動點意味著點 (x,f(x))在直線y=x上,或者換句話說,函式f的圖像與那根直線有共點。上例 f(x)=x+1的情況是,這個函式的圖像與那根直線是一對平行線。
在函式的有限次疊代之後回到相同值的點叫做周期點;不動點是周期等於 1 的周期點。
原理
不動點原理是數學上一個重要的原理,也叫壓縮映像原理或巴拿赫(Banach)不動點定理,完整的表達:完備的度量空間上,到自身的一個壓縮映射存在唯一的不動點。用初等數學可以這么理解:連續映射f的定義域包含值域,則存在一個x使得f(x)=x。
不動點的概念可以推廣到一般的拓撲空間上。 假設X是拓撲空間, f:X→X是一個連續映射, 且存在x∈X, 使得f(x)=x, 就稱x是不動點。
數學套用
1 利用f(x)的不動點解方程(牛頓切線法)
2 利用f(x)的不動點求函式或多項式的解析式
3 利用f(x)的不動點討論n-周期點問題
4 求解數列問題(求解一階遞歸數列的通項公式)
5 求解一階遞歸數列的極限
這是利用不動點開立方(牛頓切線法)的例子
開方:
公式:X(n+1)=Xn+(A/Xn^2-Xn)1/3設A=5,開3次方
5介於1^3至2^3之間(1的3次方=1,2的3次方=8)
X_0可以取1.1,1.2,1.3,1.4,1.5,1.6,1.7,1.8,1.9,2.0都可以。例如我們取2.0.按照公式:
第一步:X1={2.0+[5/(2.0^2-2.0]1/3=1.7.}。即5/2×2=1.25,1.25-2=-0.75,0.75×1/3=0.25,輸入值大於輸出值,負反饋
2-0.25=1.75,取2位數值,即1.7。
第二步:X2={1.7+[5/(1.7^2-1.7]1/3=1.71}.。
即5/1.7×1.7=1.73010,1.73-1.7=0.03,0.03×1/3=0.01,輸入值小於輸出值正反饋
1.7+0.01=1.71。取3位數,比前面多取一位數。
第三步:X3={1.71+[5/(1.71^2-1.71]1/3=1.709}輸入值大於輸出值,負反饋
第四步:X4={1.709+[5/(1.709^2-1.709]1/3=1.7099}.輸入值小於輸出值正反饋
這種方法可以自動調節,第一步與第三步取值偏大,但是計算出來以後輸出值會自動轉小;第二步,第四步輸入值偏小,輸出值自動轉大。X_4=1.7099。
當然也可以取1.1,1.2,1.3,...1.8,1.9中的任何一個。
實際套用
取一個淺盒和一張紙,紙恰好蓋住盒內的底面。可想而知此時紙上的每個點與正在它下面的盒底上的那些點配成對。把這張紙拿起來,隨機地揉成一個小球,再把小球扔進盒裡。拓撲學家已經證明,不管小球是怎樣揉成的,也不管它落在盒底的什麼地方,在揉成小球的紙上至少有一個這樣的點,它恰好處在它盒底原來配對點的正上方。
通過具體找到這個點,就能說明這個問題了。
紙被揉成球以後,看它投到紙盒底部的影子。紙盒底部的影子區域肯定比紙盒底要小。那么,就取紙盒底部的在影子內的那個部分,它肯定對應於紙團裡面的某一小團部分。(因為整個底板對應於整個紙團,那么底板的一部分就肯定對應於一部分紙團)
假如去掉紙團的其他部分,那一小團部分同樣可以在紙盒底面投影,而且投影肯定比剛才的大投影小,而且在它之內。(因為它是在整個紙團之內)。那么,取這一小片投影(注意這片影子肯定是連續的不會斷開,因為紙沒有撕裂),當它再往紙團里對應的時候,肯定對應於其中更小的一團。我們再次把多餘的紙去掉。
就是說:
整個紙盒對應於紙團
紙盒【在紙團投影內的部分】對應於紙團內的一小塊
紙盒【一小塊的投影的部分】對應於剛才那一小塊內的更小一塊
紙盒【更小塊投影的部分】對應於更小塊中的更更小一塊
…………………………
不斷地去掉紙無限次,最後紙團只剩下了一個點,它的投影就對應於紙盒的一個點。
吸引不動點
函式 f的 吸引不動點是 f的不動點 x使得,對在足夠接近 x的定義域中的任何 x值而言,疊代函式序列
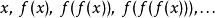 不動點
不動點收斂於 x。如何接近才是“足夠接近”有時是個微妙的問題。
自然餘弦函式(自然意味著使用弧度而非角度)有精確的一個吸引不動點。在這種情況下,“足夠接近”根本不是嚴格標準 -- 為了展示這個情況,在計算器上開始於任何實數並重複按“cos”鍵。它會快速的收斂於大約 0.73908513,這就是不動點。這是餘弦函式和線 y=x 在圖上的交叉點。
不是所有不動點都是吸引的:例如,x=0是函式 f(x)=2x 的不動點,但是這個函式對非零任意值的疊代快速的發散。
吸引不動點是更廣泛的數學概念吸引子的特殊情況。
吸引不動點被稱為 穩定不動點如果它也是李雅普諾夫穩定性的。
一個不動點被稱為是 中立穩定不動點如果它是李雅普諾夫穩定性的但不是吸引的。二階齊次線性微分方程的中心點是中立穩定不動點的例子。
定理
在數學的不同部分有很多定理保證函式、在一定的條件下,必定有一個或者更多的不動點。這些在最基本的定性結果當中,那些普遍性套用的不動點定理是非常具有價值的洞察。

