定義
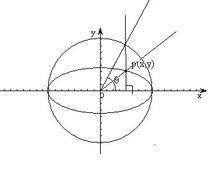 橢圓
橢圓例子
曲線的極坐標參數方程ρ=f(t),θ=g(t)。
圓的參數方程 x=a+r cosθ y=b+r sinθ(θ屬於[0,2π)) (a,b)為圓心坐標 r為圓半徑 θ為參數 (x,y)為經過點的坐標
橢圓的參數方程 x=a cosθ y=b sinθ(θ屬於[0,2π)) a為長半軸 長 b為短半軸長 θ為參數
雙曲線的參數方程 x=a secθ (正割) y=b tanθ a為實半軸長 b為虛半軸長 θ為參數
拋物線的參數方程 x=2pt^2 y=2pt p表示焦點到準線的距離 t為參數
直線的參數方程 x=x'+tcosa y=y'+tsina,x',y'和a表示直線經過(x',y'),且傾斜角為a,t為參數.
或者x=x'+ut, y=y'+vt (t屬於R)x',y'直線經過定點(x',y'),u,v表示直線的方向向量d=(u,v)
圓的漸開線x=r(cosφ+φsinφ) y=r(sinφ-φcosφ)(φ∈[0,2π)) r為基圓的半徑 φ為參數
平擺線參數方程 x=r(θ-sinθ) y=r(1-cosθ)r為圓的半徑,θ是圓的半徑所經過的角度(滾動角),當θ由0變到2π時,動點就畫出了擺線的一支,稱為一拱。
套用
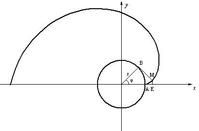 圓的漸開線
圓的漸開線柯西中值定理
如果函式f(x)及F(x)滿足:
⑴在閉區間[a,b]上連續;
⑵在開區間(a,b)內可導;
⑶對任一x∈(a,b),F'(x)≠0,
那么在(a,b)內至少有一點ζ,使等式
[f(b)-f(a)]/[F(b)-F(a)]=f'(ζ)/F'(ζ)成立。
柯西簡潔而嚴格地證明了微積分學基本定理即牛頓-萊布尼茨公式。他利用定積分嚴格證明了帶餘項的泰勒公式,還用微分與積分中值定理表示曲邊梯形的面積,推導了平面曲線之間圖形的面積、曲面面積和立體體積的公式。
參數曲線亦可以是多於一個參數的函式。例如參數表面是兩個參數(s,t)或(u,v)的函式。
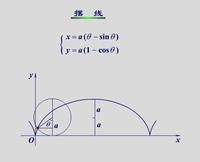 平擺線
平擺線r(u,v)=[x(u,v),y(u,v),z(u,v)]=[acos(u),asin(u),v]
參數是參變數的簡稱。它是研究運動等一類問題中產生的。質點運動時,它的位置必然與時間有關係,也就是說,質的坐標x,y與時間t之間有函式關係x=f(t),y=g(t),這兩個函式式中的變數t,相對於表示質點的幾何位置的變數x,y來說,就是一個“參與的變數”。這類實際問題中的參變數,被抽象到數學中,就成了參數。我們所學的參數方程中的參數,其任務在於溝通變數x,y及一些常量之間的聯繫,為研究曲線的形狀和性質提供方便。
用參數方程描述運動規律時,常常比用普通方程更為直接簡便。對於解決求最大射程、最大高度、飛行時間或軌跡等一系列問題都比較理想。有些重要但較複雜的曲線(例如圓的漸開線),建立它們的普通方程比較困難,甚至不可能,列出的方程既複雜又不易理解。
根據方程畫出曲線十分費時;而利用參數方程把兩個變數x,y間接地聯繫起來,常常比較容易,方程簡單明確,且畫圖也不太困難。
常見參數方程
| 過(h,k),斜率為m的直線 | 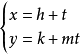 |
| 圓 | 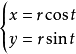 |
| 橢圓 | 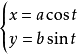 |
| 雙曲線 | 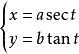 |
| 拋物線 | 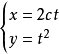 |
| 螺線 | 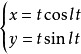 |
| 擺線 | 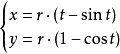 |

