單粒子與多粒子體系的相對論量子力學方程
正文
將波粒二象性觀念套用到相對論粒子體系所建立的描述粒子運動的方程。E.薛丁格曾利用這一觀念,並和波動光學進行類比,得出著名的薛丁格方程: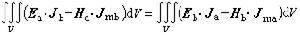 , (1)
, (1)
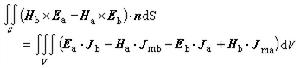 , (2)
, (2)
 是粒子的動能,U(r,t)是粒子的位能。正則對易關係提供的規則就是進行如下的替換
是粒子的動能,U(r,t)是粒子的位能。正則對易關係提供的規則就是進行如下的替換  , (3)
, (3)
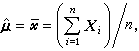 (4)
(4)
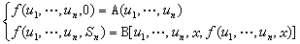 。 (5)
。 (5)
相對論量子力學歷史上的一個重要進展,是找到了
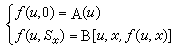 自鏇的相對論波動方程,即1928年P.A.M.狄喇克為克服克萊因-戈登方程的負幾率困難而引入的狄喇克方程。狄喇克的基本思想是:如果希望克服負幾率困難,那么在幾率密度的表示式中就必須避免引入對時間的偏導數,也就是相對論方程中的時間偏導不能高於一次。由於相對論的協變性,對空間的偏導也將限於一次。如果再要求波函式滿足線性疊加原理,那么唯一的可能性就是時空對稱的一次線性偏微分方程。此外,由於粒子還應該滿足能量動量關係式(4),因而粒子的波函式也將滿足克萊因-戈登方程(5)。正是在上述觀念指引下,狄喇克導出了一個波函式有四個分量的相對論量子力學方程:
自鏇的相對論波動方程,即1928年P.A.M.狄喇克為克服克萊因-戈登方程的負幾率困難而引入的狄喇克方程。狄喇克的基本思想是:如果希望克服負幾率困難,那么在幾率密度的表示式中就必須避免引入對時間的偏導數,也就是相對論方程中的時間偏導不能高於一次。由於相對論的協變性,對空間的偏導也將限於一次。如果再要求波函式滿足線性疊加原理,那么唯一的可能性就是時空對稱的一次線性偏微分方程。此外,由於粒子還應該滿足能量動量關係式(4),因而粒子的波函式也將滿足克萊因-戈登方程(5)。正是在上述觀念指引下,狄喇克導出了一個波函式有四個分量的相對論量子力學方程: 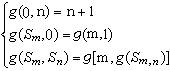 , (6)
, (6)
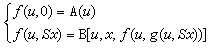
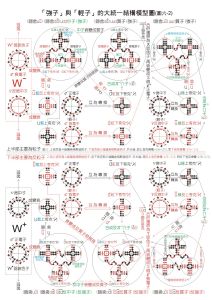 反粒子(下半圖)-內部結構模型圖
反粒子(下半圖)-內部結構模型圖曾經有一個時期認為狄喇克方程是惟一正確的相對論量子力學方程。隨著量子場論的進展,終於發現其他相對論量子力學方程也都是有物理意義的。這就進一步促使人們去探索帶有其他種自鏇的粒子所滿足的方程。質量為零、自鏇為 媡的相對論量子力學方程是人們熟知的麥克斯韋方程組,只不過對麥克斯韋方程做出粒子解釋要費事一點。特別是在坐標表象中光子波函式沒有幾率密度的概念。在麥克斯韋方程中要引進質量也沒有原則性困難。高自鏇粒子的相對論方程曾為V.巴格曼和E.P.維格納所普遍地研究過。當自鏇為
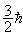 時,就得到喇里塔-施溫格方程。
時,就得到喇里塔-施溫格方程。 特別值得一提的是,對於自鏇為媡的粒子,相對論量子力學的一個重要進展是楊振寧和R.L.密耳斯於1954年提出了非阿貝耳群的規範場方程。隨著粒子物理學的進展,這類規範場方程已成為當前粒子理論研究的一個重要方向,正被廣泛地套用到電磁相互作用、弱相互作用以及強相互作用等領域。
以上所涉及的相對論量子力學方程僅限於描述一個粒子。兩個以上的粒子或多粒子體系的相對論方程就要複雜得多。原因是:①兩個以上粒子體系將能組合成任意高自鏇體系,因而多粒子的量子力學方程必須實際上包含高自鏇的巴格曼-維格納方程;②多粒子量子力學方程不僅要考慮到粒子間相互作用,而且要考慮到粒子對真空所引起的極化效應,從而間接地影響到另一些粒子的行為。按照量子場論的觀點,粒子是場的激發量子,粒子間的相互作用實質上是受量子條件的約束的場同場的相互作用,這就又必須考慮到真空中背景場所引起的間接作用。1951年,H.A.貝特和E.E.薩耳彼特利用R.P.費因曼的量子場論分析方法,克服了上述困難,提出了貝特-薩耳彼特方程,用以描述雙粒子的相對論量子力學體系。幾乎與此同時,M.蓋耳-曼、F.E.駱以及J.S.施溫格也分別用不同的方法得到了相同的方程。
以自鏇是
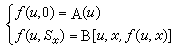 的正反粒子體系為例, 貝特-薩耳彼特方程的基本思想是:引進如下協變形式的波函式
的正反粒子體系為例, 貝特-薩耳彼特方程的基本思想是:引進如下協變形式的波函式 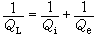 (j=1,2,3,…), (7)
(j=1,2,3,…), (7)
 (x2)是自鏇
(x2)是自鏇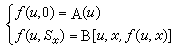 的場運算元,而ⅹj(x1,x2)是4×4的矩陣函式,其相應的方程式可寫為
的場運算元,而ⅹj(x1,x2)是4×4的矩陣函式,其相應的方程式可寫為 
 , (8)
, (8)
配圖
我曾長期研究數學,現已把在數學上取得的成果套用於建立多粒子體系的相對論波動方程,已建立了單粒子體系相對論波動方程(不含自鏇),可以精確求解,並把狄拉克方程化成二階偏微分方程形式,得到含自鏇的單粒子體系相對論波動方程,也可以精確求解.最重要的是我建立了雙粒子體系的相對論波動方程(不含自鏇)的精確形式,可近似求解,當然也許可以精確求解,但我目前做不到.成功的重要因素是引入體系質量和相對論性的約化質量,特別是通過在二階偏微分方程形式的狄拉克方程中引入相對論的約化質量,把狄拉克方程推廣到了雙粒子體系.在解雙粒子體系的相對論波動方程後,除了得到對應原子光譜的能級外,還得到了一種反常能級,這種反常能級正好解釋粒子的成對產生和成對湮滅,好像還有助於人們理解真空的本質,包括真空極化和真空電磁漲落.說反常是因為這種能級是隨主量子數的增大而降低的.對於電子偶素,當主量子數趨於無窮大時,這種反常能級的能量值趨於零,這就定量地說明了電子偶素的定態能級中存在真空態,證明了電子正電子對的湮滅和產生就是電子偶素的能級躍遷.因此,只要引入體系質量的概念,線性偏微分方程形式的相對論量子力學方程也能描寫粒子的產生和湮滅.
任何一個粒子,都處於跟其它粒子的相互作用狀態和運動狀態,它的真實質量並不等於其靜止質量,因此,描述粒子的相對論量子力學方程必定是與粒子的真實質量有關的.最早出現的相對論量子力學方程是Klein-Gordon方程和Dirac方程,但出現在方程表達式中的粒子質量卻只有靜止質量,這是為什麼呢?粒子的靜止質量對應於Lorentz標量,這使Klein-Gordon方程和Dirac方程具有明顯的Lorentz協變性,但這並不排除方程還具有另一種等價形式,一種與粒子的真實質量密切相關的形式.體系質量就是體系的真實質量.顯然,原子核的真實質量明顯小於構成它的各個核子的靜止質量之和.因此,引入體系質量概念,並把它跟構成體系的各個粒子的靜止質量之和區分開來是非常重要的.體系質量的引入,首先可以消除Klein-Gordon方程的負幾率困難,並為建立多粒子體系的相對論量子力學方程創造條件.
我(本人真實名字:畢光慶)的單粒子體系的相對論量子力學方程是:
iħ(∂/∂t)Ψ=–ħ²▽²Ψ/(m0+m)+2mUΨ/(m0+m)–U²Ψ/(m0+m)c²
式中m0為粒子的靜止質量,m為粒子在勢場U中運動時的實際質量.並且可以給出確定的法則使若知道一個慣性系中的波函式,就可以計算出另一個慣性系中的波函式.
當式中的U為零時,方程就成為Klein-Gordon方程的等價形式,但這種等價形式不存在負幾率因難.這裡關鍵是在方程中引入了體系的實際質量,我稱之為體系質量.我們常說的原子核質量就是指原子核的體系質量,它小於構成原子核的各個核子的靜止質量之和,其差值為體系(原子核)的質量虧損.因此,體系質量概念的引入克服了Klein-Gordon方程的負幾率困難.當我把這個方程套用於類氫離子體系時,方程中含U的平方的項正好給出了用基本電荷和普朗克常數及光速三者表示的精細結構常數.作為這個方程的作者,這是我事先沒有想到的,也感到非常驚奇.這個方程的優點之一是比較容易精確求解,得到的類氫離子的定態能級公式幾乎跟Dirac方程得到的一樣.建立這個方程的基本假設只有兩條,一是量子力學的態疊加原理,它本身是相對論的,一是相對論的能量動量關係式.顯然這兩條原理的正確性早就不是問題.長期的數學研究使我積累了一定的數學基礎,推導中所用的數學技巧也是不成問題的.最重要的是通過引入相對論的約化質量概念,我們還可以進一步建立雙粒子體系的相對論量子力學方程..
