定理內容
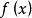積分中值定理若函式
在閉區間
上連續,，則在積分區間
上至少存在一個點
，使下式成立
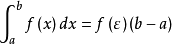積分中值定理
積分中值定理其中，a、b、
滿足：a≤
≤b。
定理證明
證明的方法有很多種，這裡給出最常見的一種。
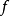積分中值定理設
在
上的最大值為
，最小值為
，
積分中值定理① 若
，則
，
可取任意值。
積分中值定理① 若
，則
，有
，故有：
，即：
積分中值定理同理有：
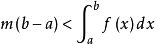積分中值定理
積分中值定理由連續函式的介值定理可知，必定
，使得
，即：
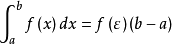積分中值定理命題得證。
幾何意義
積分中值定理這個定理的幾何意義為:若
，
，則由
軸、
、
及曲線
圍成的曲邊梯形的面積等於一個長為
，寬為
的矩形的面積。
推廣形式
第一定理
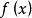積分中值定理如果函式
、
在閉區間
上可積，且
在
上不變號,f(x)連續， 則在積分區間
上至少存在一個點
，使下式成立：
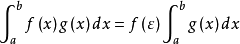積分中值定理第二定理
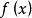積分中值定理一、如果函式
、
在閉區間
上可積，且
為單調函式，則在積分區間
上至少存在一個點
,，使下式成立：
積分中值定理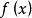積分中值定理二、如果函式
、
在閉區間[a,b]上可積，且
並是單調遞減函式，則在積分區間
上至少存在一個點
， 使下式成立：
積分中值定理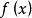積分中值定理三、如果函式
、
在閉區間
上可積，且
並是單調遞增函式，則在積分區間
上至少存在一個點
，使下式成立：
積分中值定理定理套用
積分中值定理在套用中所起到的重要作用是可以使積分號去掉，或者使複雜的被積函式化為相對簡單的被積函式，從而使問題簡化。因此，對於證明有關題設中含有某個函式積分的等式或不等式，或者要證的結論中含有定積分，或者所求的極限式中含有定積分時，一般應考慮使用積分中值定理， 去掉積分號，或者化簡被積函式。
求極限
在函式極限的計算中, 如果含有定積分式, 常常可以運用定積分的相關知識, 比如積分中值定理等, 把積分
積分中值定理問題運用
某些帶積分式的函式, 常常會有要求判定某些性質的點的存在的問題, 有時運用積分中值定理能使問題迎刃而解。
例題2運用估計
在大多數的積分式中, 能找到其被積函式的原函式再進行求值的積分簡直是鳳毛麟角, 當被積函式“積不出”或者原函式很複雜時, 可用各種方法來估計積分。對於乘積型的被積函式, 將變化緩慢的部分或積分困難的部分進行估計, 可積的部分積分之。積分中值定理和各種不等式就是其中常用的方法,
例題3不等式證明
積分不等式是指不等式中含有兩個以上積分的不等式,當積分區間相同時,先合併同一積分區間上的不同積分,根據被積函式所滿足的條件,靈靈活運用積分中值定理,以達到證明不等式成立的目的。
在證明定積分不等式時, 常常考慮運用積分中值定理, 以便去掉積分符號, 如果被積函式是兩個函式之積時, 可考慮用積分第一或者第二中值定理。對於某些不等式的證明, 運用原積分中值定理只能得到“≥”的結論, 或者不等式根本不能得到證明。而運用改進了的積分中值定理之後, 則可以得到“>”的結論, 或者成功的解決問題。
例題4