弗雷德霍姆積分方程
正文
形如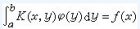 1
1(1)
和
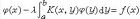 2
2(2)
的積分方程,依次稱為第一種弗雷德霍姆積分方程和第二種弗雷德霍姆積分方程,其中λ 是參數,φ(x)是未知函式,核K(x,y)和自由項 ƒ(x)是預先給定的函式。通常假設 K(x,y)屬於平方絕對可積函式類,記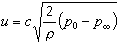
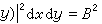 ,B是非負數。當ƒ(x)恆為零時,稱為齊次積分方程,否則稱為非齊次積分方程。
,B是非負數。當ƒ(x)恆為零時,稱為齊次積分方程,否則稱為非齊次積分方程。
逐次逼近法及解核 第二種弗雷德霍姆積分方程的最簡便的一種解法是逐次逼近法,即按遞推公式
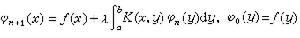
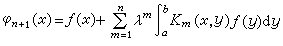 ,
,
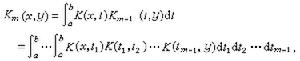 易知,
易知, 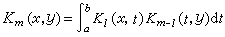 ,
,
若級數
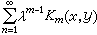 一致收斂,記之為Γ(x,y;λ),則Γ(x,y;λ)同時滿足下面兩個方程:
一致收斂,記之為Γ(x,y;λ),則Γ(x,y;λ)同時滿足下面兩個方程: 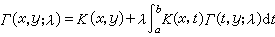 , (3)
, (3)
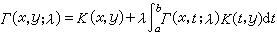 , (4)
, (4)
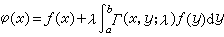 , (5)
, (5)
對於解核不存在的值 λ,稱為特徵值。否則,稱為正則值。若且唯若λ是特徵值時,對應的齊次方程
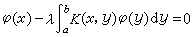 (6)
(6)
弗雷德霍姆方法 E.I.弗雷德霍姆給出了一般情形的解核構造法。設 K(x,y)是有界核,即│K(x,y)│<M(M 是實常數),記
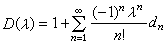 , (7)
, (7)
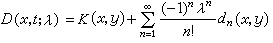 , (8)
, (8)
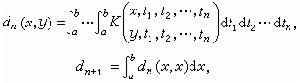
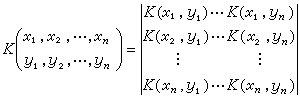 。
。
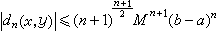 ,從而推知級數(7)、(8)對於一切復值 λ是絕對一致收斂的,因此,D(λ)、D(x,y;λ)都是關於λ的整函式,並分別稱為弗雷德霍姆行列式和弗雷德霍姆一階子式。可以證明,解核可表為Г(x,y;λ)=D(x,y;λ)/D(λ)。這表明解核是λ的半純函式。同時,解核的極點都是 D(λ)的零點,也都是齊次方程(6)的特徵值。反之亦然。
,從而推知級數(7)、(8)對於一切復值 λ是絕對一致收斂的,因此,D(λ)、D(x,y;λ)都是關於λ的整函式,並分別稱為弗雷德霍姆行列式和弗雷德霍姆一階子式。可以證明,解核可表為Г(x,y;λ)=D(x,y;λ)/D(λ)。這表明解核是λ的半純函式。同時,解核的極點都是 D(λ)的零點,也都是齊次方程(6)的特徵值。反之亦然。 弗雷德霍姆定理 弗雷德霍姆對於第二種積分方程的研究,可歸結為如下的四個定理,總稱為弗雷德霍姆定理。它是弗雷德霍姆積分方程理論的基礎。
第一定理 在λ複平面的任意有限區域內,方程(2)至多只有有限個特徵值。
第二定理 每個特徵值λ至少對應於一個特徵函式,且所對應的線性無關的特徵函式的個數是有限的。這個有限數稱為λ的秩。
第三定理 設λ是核K(x,y)的特徵值,則 憳是共軛核
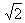 的特徵值。齊次方程 (6)與其共軛齊次方程
的特徵值。齊次方程 (6)與其共軛齊次方程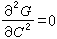 具有相同的秩。
具有相同的秩。 第四定理 若λ是核K(x,y)的特徵值,則非齊次方程(2)可解的充分必要條件為:方程(2)的自由項ƒ(x)與其共軛齊次方程的所有線性無關解ψi(x)正交,即
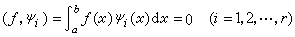 ,
,
因此,非齊次方程(2),或者對任意自由項可解,或者相應的齊次方程有非零解。這一結論通常稱為弗雷德霍姆備擇定理。
對於第一種弗雷德霍姆積分方程,若φ(x)是它的解,又有非零的任意函式ψ(x)使得
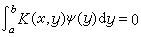 ,則φ(x)+ψ(x)也是它的解。E.施密特對方程(1)的特徵值和特徵函式給出了如下的定義:若對於某實數 λ存在非零的函式φ(x)和ψ(x),滿足方程組
,則φ(x)+ψ(x)也是它的解。E.施密特對方程(1)的特徵值和特徵函式給出了如下的定義:若對於某實數 λ存在非零的函式φ(x)和ψ(x),滿足方程組 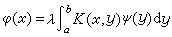 ,
,
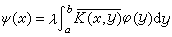 ,
,
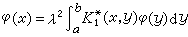 ,
,
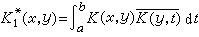 ;
;
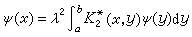 ,
,
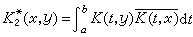 。
。
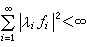 式中ƒi=(ƒ,φ)。以後,(C.-)É.皮卡進而證明,在正交標準特徵函式系{φi(x)}是完備的情形,這條件也是充分的。此即所謂施密特-皮卡定理。
式中ƒi=(ƒ,φ)。以後,(C.-)É.皮卡進而證明,在正交標準特徵函式系{φi(x)}是完備的情形,這條件也是充分的。此即所謂施密特-皮卡定理。 對於第一種弗雷德霍姆積分方程的研究,近代有了新的進展,並提供了一些有效的解法,但至今還未建立起系統的理論。