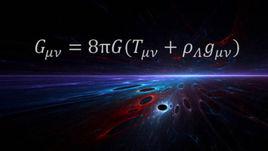概念介紹
黑洞
愛因斯坦的廣義相對論理論在天體物理學中有著非常重要的套用:它直接推導出某些大質量恆星會終結為一個黑洞——時空中的某些區域發生極度的扭曲以至於連光都無法逸出;而多大質量的恆星會塌陷為黑洞則是印裔物理學家錢德拉塞卡的功勞——錢德拉塞卡極限(白矮星的質量上限)。
引力透像
有證據表明恆星質量黑洞以及超大質量黑洞是某些天體例如活動星系核和微類星體發射高強度輻射的直接成因。光線在引力場中的偏折會形成引力透鏡現象,這使得人們能夠觀察到處於遙遠位置的同一個天體的多個成像。
引力波
廣義相對論還預言了引力波的存在(愛因斯坦於1918年寫的論文《論引力波》),現已被直接觀測所證實。此外,廣義相對論還是現代宇宙學的膨脹宇宙模型的理論基礎。
時空關係
19世紀末由於牛頓力學和(蘇格蘭數學家)麥克斯韋(1831~1879年)電磁理論趨於完善,一些物理學家認為“物理學的發展實際上已經結束”,但當人們運用伽利略變換解釋光的傳播等問題時,發現一系列尖銳矛盾,對經典時空觀產生疑問。愛因斯坦對這些問題,提出物理學中新的時空觀,建立了可與光速相比擬的高速運動物體的規律,創立相對論。 狹義相對論提出兩條基本原理。(1) 光速不變原理:即在任何 慣性系中, 真空中光速c都相同,為299,792,458m/s,與光源及觀察者的運動狀況無關。(2)狹義相對性原理:是指物理學的基本定律乃至自然規律,對所有慣性參考系來說都相同。
愛因斯坦的第二種相對性理論(1916年)。該理論認為引力是由空間——時間彎曲的幾何效應(也就是,不僅考慮空間中的點之間,而是考慮在空間和時間中的點之間距離的幾何)的畸變引起的,因而引力場影響時間和距離的測量。
萬有引力
廣義相對論:是一種關於萬有引力本質的理論。愛因斯坦曾經一度試圖把萬有引力定律納入相對論的框架,幾經失敗後,他終於認識到,狹義相對論容納不了萬有引力定律。於是,他將狹義相對性原理推廣到廣義相對性,又利用在局部慣性系中萬有引力與慣性力等效的原理,建立了用彎曲時空的黎曼幾何描述引力的廣義相對論理論。
狹義相對論
狹義相對論與廣義相對論:狹義相對論只適用於慣性系,它的時空背景是平直的四維時空,而廣義相對論則適用於包括非慣性系在內的一切參考系,它的時空背景是彎曲的黎曼時空。
誕生背景
發展過程
愛因斯坦在1905年發表了一篇探討光線在狹義相對論中,重力和加速度對其影響的論文,廣義相對論的雛型就此開始形成。1912年,愛因斯坦發表了另外一篇論文,探討如何將重力場用幾何的語言來描述。至此,廣義相對論的運動學出現了。到了1915年, 愛因斯坦引力場方程發表了出來,整個廣義相對論的動力學才終於完成。
開場方程式解
1915年後,廣義相對論的發展多集中在解開場方程式上,解答的物理解釋以及尋求可能的實驗與觀測也占了很大的一部份。但因為場方程式是一個非線性偏微分方程,很難得出解來,所以在電腦開始套用在科學上之前,也只有少數的解被解出來而已。其中最著名的有三個解:史瓦西解、 雷斯勒——諾斯特朗姆解、克爾解。
三大驗證
在廣義相對論的實驗驗證上,有著名的三大驗證。在水星近日點的進動中,每百年43秒的剩餘進動長期無法得到解釋,被廣義相對論完滿地解釋清楚了。光線在引力場中的彎曲,廣義相對論計算的結果比牛頓理論正好大了1倍,愛丁頓和戴森的觀測隊利用1919年5月29日的日全食進行觀測的結果,證實了廣義相對論是正確的。再就是引力紅移,按照廣義相對論,在引力場中的時鐘要變慢,因此從恆星表面射到地球上來的光線,其光譜線會發生紅移,這也在很高精度上得到了證實。從此,廣義相對論理論的正確性被得到了廣泛地承認。
另外,宇宙的膨脹也創造出了廣義相對論的另一場高潮。從1922年開始,研究者們就發現場方程式所得出的解答會是一個膨脹中的宇宙,而愛因斯坦在那時自然也不相信宇宙會來漲縮,所以他便在場方程式中加入了一個宇宙常數來使場方程式可以解出一個穩定宇宙的解出來。但是這個解有兩個問題。在理論上,一個穩定宇宙的解在數學上不是穩定。另外在觀測上,1929年,哈勃發現了宇宙其實是在膨脹的,這個實驗結果使得愛因斯坦放棄了宇宙常數,並宣稱這是我一生最大的錯誤(the biggest blunder in my career)。
但根據最近的一形超新星的觀察,宇宙膨脹正在加速。所以宇宙常數似乎有再度復活的可能性,宇宙中存在的暗能量可能就必須用宇宙常數來解釋.
基本假設
簡單地說,廣義相對論的兩個基本原理是:一,等效原理:慣性力場與引力場的動力學效應是 局部不可分辨的 ;二,廣義相對性原理:所有的物理定律在任何參考系中都取相同的形式。
原理
等效原理:分為弱等效原理和強等效原理,弱等效原理認為慣性力場與引力場的動力學效應是局部不可分辨的。強等效原理認為,則將“動力學效應”提升到“任何物理效應”。要強調, 等效原理僅對局部慣性系成立, 對非局部慣性系等效原理不一定成立。
廣義相對性原理:物理定律的形式在一切參考系都是不變的。該定理是狹義相對性原理的推廣。在狹義相對論中,如果我們嘗試去定義慣性系,會出現死循環:一般地,不受外力的物體,在其保持靜止或勻速直線運動狀態不變的坐標系是慣性系;但如何判定物體不受外力?回答只能是,當物體保持靜止或勻速直線運動狀態不變時,物體不受外力。很明顯,邏輯出現了難以消除的死循環。這說明對於慣性系,人們無法給出嚴格定義,這不能不說是狹義相對論的嚴重缺憾。為了解決這個問題,愛因斯坦直接將慣性系的概念從相對論中剔除,用“任何參考系”代替了原來狹義相對性原理中“慣性系”。
廣義相對論是基於狹義相對論的。如果後者被證明是錯誤的,整個理論的大廈都將垮塌。
 愛因斯坦解釋廣義相對論的手稿扉頁
愛因斯坦解釋廣義相對論的手稿扉頁為了理解廣義相對論,我們必須明確質量在經典力學中是如何定義的。首先,讓我們思考一下質量在日常生活中代表什麼。“它是重量”?事實上,我們認為質量是某種可稱量的東西,正如我們是這樣度量它的:我們把需要測出其質量的物體放在一架天平上。我們這樣做是利用了質量的什麼性質呢?是地球和被測物體相互吸引的事實。這種質量被稱作“引力質量
”(m1:m2=F1:F2)。我們稱它為“引力的”是因為它決定了宇宙中所有星星和恆星的運行:地球和太陽間的引力質量驅使地球圍繞後者作近乎圓形的環繞運動。
試著在一個平面上推你的汽車。你不能否認你的汽車強烈地反抗著你要給它的加速度。這是因為你的汽車有一個非常大的質量。移動輕的物體要比移動重的物體輕鬆。質量也可以用另一種方式定義:“它反抗加速度”。這種質量被稱作“慣性質量”(m=F/a,注:這不是牛頓定律,只是一種測量質量的方法)。
因此我們得出這個結論:我們可以用兩種方法度量質量。要么我們稱它的重量(非常簡單),要么我們測量它對加速度的抵抗(使用力與加速度的比值)。
引力質量與慣性質量
人們做了許多實驗以測量同一物體的慣性質量和引力質量。所有的實驗結果都得出同一結論:慣性質量等於引力質量(實際上是成正比,調整係數後,就變成"等於"了,這么做是為了方便計算)。
牛頓自己意識到這種質量的等同性是由某種他的理論不能夠解釋的原因引起的。但他認為這一結果是一種簡單的巧合。與此相反,愛因斯坦發現這種等同性中存在著一條取代牛頓理論的通道。
日常經驗驗證了這一等同性:兩個物體(一輕一重)會以相同的速度“下落”。然而重的物體受到的地球引力比輕的大。那么為什麼它不會“落”得更快呢?因為它對加速度的抵抗更強。結論是,引力場中物體的加速度與其質量無關。伽利略是第一個注意到此現象的人。重要的是你應該明白,引力場中所有的物體“以同一加速度下落”是(經典力學中)慣性質量和引力質量等同的結果。
關注一下“下落”這個表述。物體“下落”是由於地球的引力質量產生了地球的引力場。兩個物體在所有相同的引力場中的加速度相同。不論是月亮的還是太陽的,它們以相同的比率被加速。這就是說它們的速度在每秒鐘內的增量相同。(加速度是速度每秒的增加值)
引力質量和慣性質量的等同性
愛因斯坦一直在尋找“引力質量與慣性質量相等”的解釋。為了這個目標,他作出了被稱作“等同原理”的第三假設。它說明:如果一個慣性系相對於一個伽利略系被均勻地加速,那么我們就可以通過引入相對於它的一個均勻引力場而認為它(該慣性系)是靜止的。
讓我們來考查一個慣性系K’,它有一個相對於伽利略系的均勻加速運動。在K 和K’周圍有許多物體。此物體相對於K是靜止的。因此這些物體相對於K’有一個相同的加速運動。這個加速度對所有的物體都是相同的,並且與K’相對於K的加速度方向相反。我們說過,在一個引力場中所有物體的加速度的大小都是相同的,因此其效果等同於K’是靜止的並且存在一個均勻的引力場。
因此如果我們確立等同原理,物體的兩種質量相等只是它的一個簡單推論。 這就是為什麼(質量)等同是支持等同原理的一個重要論據。
第四個原理
通過假定K’靜止且引力場存在,我們將K’理解為一個伽利略系,(這樣我們就可以)在其中研究力學規律。由此愛因斯坦確立了他的第四個原理。
理論內容
等效原理
愛因斯坦提出“等效原理”,即引力和慣性力是等效的。這一原理建立在引力質量與慣性質量的等價性上。根據等效原理,愛因斯坦把狹義相對性原理推廣為廣義相對性原理,即物理定律的形式在一切參考系都是不變的。物體的運動方程即該參考系中的測地線方程。測地線方程與物體自身固有性質無關,只取決於時空局域幾何性質。而引力正是時空局域幾何性質的表現。物質質量的存在會造成時空的彎曲,在彎曲的時空中,物體仍然順著最短距離進行運動(即沿著測地線運動——在歐氏空間中即是直線運動),如地球在太陽造成的彎曲時空中的測地線運動,實際是繞著太陽轉,造成引力作用效應。正如在彎曲的地球表面上,如果以直線運動,實際是繞著地球表面的大圓走。
幾何基礎
引力是時空局域幾何性質的表現。雖然廣義相對論是愛因斯坦創立的,但是它的數學基礎的源頭可以追溯到歐氏幾何的公理和數個世紀以來為證明歐幾里德第五公設(即平行線永遠保持等距)所做的努力,這方面的努力在羅巴切夫斯基、波爾約、高斯的工作中到達了頂點:他們指出歐氏第五公設是不能用前四條公設證明的。非歐幾何的一般數學理論是由高斯於1827年完成的(1828年發表),他在研究曲面的性質時不再藉助外圍空間,而直接將曲面作為研究對象,創立了曲面的“內蘊”幾何學。1854年,高斯的學生黎曼將高斯的內蘊幾何學推廣到高維空間,建立起任意維度的彎曲空間的幾何學基礎,被稱為黎曼幾何,在愛因斯坦發展出廣義相對論之前,絕大多數人認為非歐幾何是無法套用到真實世界中來的。
愛因斯坦場方程以及史瓦西解
在廣義相對論中,引力的作用被“幾何化”——即是說:狹義相對論的閔氏空間背景加上萬有引力的物理圖景在廣義相對論中變成了黎曼空間背景下不受力(假設沒有電磁等相互作用)的自由運動的物理圖景,其動力學方程與自身質量無關而成為測地線方程。
引力場方程是一個非常複雜的二階偏微分方程,有16個自變數。
具體形式如下:
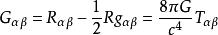 廣義相對論
廣義相對論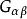 廣義相對論
廣義相對論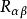 廣義相對論
廣義相對論 廣義相對論
廣義相對論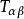 廣義相對論
廣義相對論式子中 代表 愛因斯坦張量, 代表黎曼曲率張量縮並後的 里奇(Ricci)張量, 代表曲率標量, 為能量動量張量。
這個方程用來描述 引力場的具體情況,由於它是一個二階非線性偏微分方程組,所以求起來很麻煩,第一個獲得該方程解的是史瓦西,他在默認引力場是靜態的情況下,用 真空場方程
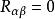 廣義相對論
廣義相對論算得 克氏符的非零分量,求得了空間函式的具體表達形式,史瓦西解的具體形式如下
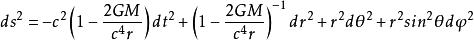 廣義相對論
廣義相對論 廣義相對論
廣義相對論 廣義相對論
廣義相對論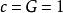 廣義相對論
廣義相對論上面的度規中 代表引力源的質量, 為萬有引力常數,若採取幾何單位制( ),則改度規可化簡
利用上述的 度規可以得出引力對時間的影響。
預言
按照廣義相對論,在局部慣性系內,不存在引力,一維時間和三維空間組成四維平坦的歐幾里得空間;在任意參考系內,存在引力,引力引起時空彎曲,因而時空是四維彎曲的非歐黎曼空間。愛因斯坦找到了物質分布影響時空幾何的引力場方程。時間空間的彎曲結構取決於物質能量密度、動量密度在時間空間中的分布,而時間空間的彎曲結構又反過來決定物體的運動軌道。在引力不強、時間空間彎曲很小情況下,廣義相對論的預言同牛頓萬有引力定律和牛頓運動定律的預言趨於一致;而引力較強、時間空間彎曲較大情況下,兩者有區別。廣義相對論提出以來,預言了水星近日點反常進動、光頻引力紅移、光線引力偏折以及雷達回波延遲,都被天文觀測或實驗所證實。關於脈衝雙星的觀測也提供了有關廣義相對論預言存在引力波的有力證據。
愛因斯坦提出了革命性的思想,即引力不像其他種類的力,它只不過是時空不是平坦的這一事實的結果,而早先人們假定時空是平坦的。像地球這樣的物體並非由於稱為引力的力使之沿著彎曲軌道運動,相反,它沿著彎曲空間中最接近於直線路徑的東西運動,這個東西稱為測地線。一根測地線是臨近兩點之間最短(或最長)的路徑。在廣義相對論中,物體總是沿著四維時空的直線走。儘管如此,在我們看來它在三維空間中是沿著彎曲的路徑。(這正如同看一架在非常多山的地面上空飛行的飛機。雖然它沿著三維時空的直線飛,它在二維的地面上的影子卻是沿著一條彎曲的路徑。)廣義相對論的另一個預言是,在像地球這樣的大質量的物體附近,時間顯得流逝得更慢一些。這是因為光能量和它的頻率(光在每秒鐘里搏動的次數)有一種關係:能量越大,則頻率越高。當光從地球的引力場往上行進,它失去能量,因而其頻率下降(這表明兩個相鄰波峰之間的時間間隔變大。)在上面的某個人看來,下面發生的每一件事情都顯得需要更長的時間。1962年,人們利用一對安裝在水塔頂上和底下的非常準確的鐘,驗證了這個預言,發現底下那隻更接近地球的鐘走得比較慢。 牛頓運動定律使在空間中的絕對位置的觀念壽終正寢,而相對論擺脫了絕對時間。考慮一對雙生子。假定其中一個孩子去山頂上生活,而另一個留在海平面,第一個將比第二個老得快些。這叫做雙生子佯謬,但是,只是對於頭腦中仍有絕對時間觀念的人而言,這才是佯謬。在相對論中並沒有唯一的絕對時間,相反,每個人都有他自己的時間測度,這依賴於他在何處並如何運動。
套用
廣義相對論由於它被令人驚嘆地證實以及其理論上的優美,很快得到人們的承認和讚賞。然而由於牛頓引力理論對於絕大部分引力現象已經足夠精確,廣義相對論只提供了一個極小的修正,人們在實用上並不需要它,因此,廣義相對論建立以後的半個世紀,並沒有受到充分重視,也沒有得到迅速發展。到20世紀60年代,情況發生變化,發現強引力天體(中子星)和3K宇宙背景輻射,使廣義相對論的研究蓬勃發展起來。廣義相對論對於研究天體結構和演化以及宇宙的結構和演化具有重要意義。中子星的形成和結構、黑洞物理和黑洞探測、引力輻射理論和引力波探測、大爆炸宇宙學、量子引力以及大尺度時空的拓撲結構等問題的研究正在深入,廣義相對論成為物理研究的重要理論基礎。
實驗檢驗
水星近日點進動
1859年,天文學家勒威耶(Le Verrier)發現水星近日點進動的觀測值,比根據牛頓定律計算的理論值每百年快38角秒。他猜想可能在水星以內還有一顆小行星,這顆小行星對水星的引力導致兩者的偏差。可是經過多年的搜尋,始終沒有找到這顆小行星。1882年,紐康姆(S.Newcomb)
經過重新計算,得出水星近日點的多餘進動值為每百年43角秒。他提出,有可能是水星因發出黃道光的瀰漫物質使水星的運動受到阻力。但這又不能解釋為什麼其他幾顆行星也有類似的多餘進動。紐康姆於是懷疑引力是否服從平方反比定律。後來還有人用電磁理論來解釋水星近日點進動的反常現象,都未獲成功。
1915年,愛因斯坦根據廣義相對論把行星的繞日運動看成是它在太陽引力場中的運動,由於太陽的質量造成周圍空間發生彎曲,使行星每公轉一周近日點進動為:
ε=24π2a2/T2c2(1-e2)
其中a為行星軌道的長半軸,c為光速,以cm/s表示,e為偏心率,T為公轉周期。對於水星,計算出ε=43″/百年,正好與紐康姆的結果相符,一舉解決了牛頓引力理論多年未解決的懸案。這個結果當時成了廣義相對論最有力的一個證據。水星是最接近太陽的內行星。離中心天體越近,引力場越強,時空彎曲的曲率就越大。再加上水星運動軌道的偏心率較大,所以進動的修正值也比其他行星為大。後來測到的金星,地球和小行星伊卡魯斯的多餘進動跟理論計算也都基本相符。
光線在引力場中的彎曲
1911年愛因斯坦在《引力對光傳播的影響》一文中討論了光線經過太陽附近時由於太陽引力的作用會產生彎曲。他推算出偏角為0.83″,並且指出這一現象可以在日全食進行觀測。1914年德國天文學家弗勞德(E.F.Freundlich)領隊去克里木半島準備對當年八月間的日全食進行觀測,正遇上第一次世界大戰爆發,觀測未能進行。幸虧這樣,因為愛因斯坦當時只考慮到等價原理,計算結果小了一半。1916年愛因斯坦根據完整的廣義相對論對光線在引力場中的彎曲重新作了計算。他不僅考慮到太陽引力的作用,還考慮到太陽質量導致空間幾何形變,光線的偏角為:α=1″.75R0/r,其中R0為太陽半徑,r為光線到太陽中心的距離。
1919年日全食期間,英國皇家學會和英國皇家天文學會派出了由愛丁頓(A.S.Eddington)等人率領的兩支觀測隊分赴西非幾內亞灣的普林西比島(Principe)和巴西的索布臘兒爾(Sobral)兩地觀測。經過比較,兩地的觀測結果分別為1″.61±0″.30和1″.98±0″.12。把當時測到的偏角數據跟愛因斯坦的理論預期比較,基本相符。這種觀測精度太低,而且還會受到其他因素的干擾。人們一直在找日全食以外的可能。20世紀60年代發展起來的射電天文學帶來了希望。用射電望遠鏡發現了類星射電源。1974年和1975年對類星體觀測的結果,理論和觀測值的偏差不超過百分之一。
光譜線的引力紅移
廣義相對論指出,在強引力場中時鐘要走得慢些,因此從巨大質量的星體表面發射到地球上的光線,會向光譜的紅端移動。愛因斯坦1911年在《引力對光傳播的影響》一文中就討論了這個問題。他以Φ表示太陽表面與地球之間的引力勢差,ν0、ν分別表示光線在太陽表面和到達地球時的頻率,得:
(ν0 -ν)/ν=-Φ/c2=2×10-6.
 行星繞恆星作公轉的比較
行星繞恆星作公轉的比較愛因斯坦指出,這一結果與法布里(C.Fabry)等人的觀 測相符,而法布里當時原來還以為是其它原因的影響。
1925年,美國威爾遜山天文台的亞當斯(W.S.Adams)觀測了天狼星的伴星天狼A。這顆伴星是所謂的白矮星,其密度比鉑大二千倍。觀測它發出的譜線,得到的頻移與廣義相對論的預期基本相符。
1958年,穆斯堡爾效應得到發現。用這個效應可以測到解析度極高的r射線共振吸收。1959年,龐德(R.V.Pound)和雷布卡(G.Rebka)首先提出了運用穆斯堡爾效應檢測引力頻移的方案。接著,他們成功地進行了實驗,得到的結果與理論值相差約百分之五。
用原子鐘測引力頻移也能得到很好的結果。1971年,海菲勒(J.C.Hafele)和凱丁(R.E.Keating)用幾台銫原子鐘比較不同高度的計時率,其中有一台置於地面作為參考鍾,另外幾台由民航機攜帶登空,在1萬米高空沿赤道環繞地球飛行。實驗結果與理論預期值在10%內相符。1980年魏索特(R.F.C.Vessot)等人用氫原子鐘做實驗。他們把氫原子鐘用火箭發射至一萬公里太空,得到的結果與理論值相差只有±7×10^-5。
雷達回波延遲
光線經過大質量物體附近的彎曲現象可以看成是一種折射,相當於光速減慢,因此從空間某一點發出的信號,如果途經太陽附近,到達地球的時間將有所延遲。1964年,夏皮羅(I.I.Shapiro)首先提出這個建議。他的小組先後對水星、金星與火星進行了雷達實驗,證明雷達回波確有延遲現象。開始有人用人造天體作為反射靶,實驗精度有所改善。這類實驗所得結果與廣義相對論理論值比較,相差大約1%。用天文學觀測檢驗廣義相對論的事例還有許多。例如:引力波的觀測和雙星觀測,有關宇宙膨脹的哈勃定律,黑洞的發現,中子星的發現,微波背景輻射的發現等等。通過各種實驗檢驗,廣義相對論越來越令人信服。然而,有一點應該特彆強調:我們可以用一個實驗否定某個理論,卻不能用有限數量的實驗最終證明一個理論;一個精確度並不很高的實驗也許就可以推翻某個理論,卻無法用精確度很高的一系列實驗最終肯定一個理論。對於廣義相對論的是否正確,人們必須採取非常謹慎的態度,嚴格而小心地作出合理的結論。
第四假設
愛因斯坦的第四假設是其第一假設的推廣。它可以這樣表述:自然法則在所有的系中都是相同的。
不可否認,宣稱所有系中的自然規律都是相同的比稱只有在伽利略系中自然規律相同聽起來更“自然”。但是我們不知道(外部)是否存在一個伽利略系。
這個原理被稱作“廣義相對論原理”
死亡電梯
讓我們假想一個在摩天大樓內部自由下落的電梯,裡面有一個蠢人。 這人讓他的表和手絹同時落下。會發生什麼呢?對於一個電梯外以地球為參照系的人來說,表、手絹、人和電梯正以完全一致的速度下落。(讓我們複習一下:依據等同性原理,引力場中物體的運動不依賴於它的質量。)所以表和地板,手絹和地板,人和表,人和手絹的距離固定不變。因此對於電梯裡的人而言,表和手絹將呆在他剛才扔它們的地方。
如果這人給他的手錶或他的手絹一個特定的速度,它們將以恆定的速度沿直線運動。電梯表現得像一個伽利略系。然而,這不會永遠持續下去。遲早電梯都會撞碎,電梯外的觀察者將去參加一個意外事故的葬禮。
我們來做第二個理想化的試驗:我們的電梯遠離任何大質量的物體。比如,正在宇宙深處。我們的大蠢蛋從上次事故中逃生。他在醫院呆了幾年後,決定重返電梯。突然一個生物開始拖動這個電梯。經典力學告訴我們:恆力將產生恆定的加速度。(由於一個物體的質量隨速度的增加而增大,所以為了產生恆定的加速度,所加的恆力也必須隨質量的增大而增大。當物體的速度接近光速時,物體的質量將趨於無限大。)由此,電梯在伽利略系中將有一個加速運動。
我們的天才傻瓜呆在電梯裡讓他的手絹和手錶下落。電梯外伽利略系中的人認為手錶和手絹會撞到地板上。這是由於地板因其加速度而向它們(手絹和手錶)撞過來。事實上,電梯外的人將會發現表和地板以及手絹和地板間的距離以相同的速率在減小。另一方面,電梯裡的人會注意到他的手錶和手絹有相同的加速度,他會把這歸因於引力場。
這兩種解釋看起來似乎一樣:一邊是一個加速運動,另一邊是一致的運動和引力場。
讓我們再做一個實驗來證明引力場的存在。一束光通過窗戶射在對面的牆上。我們的兩位觀察者是這樣解釋的:
在電梯外的人告訴我們:光通過窗戶以恆定的速度(當然了!)沿一條直線水平地射進電梯,照在對面的牆上。但由於電梯正在向上運動,所以光線的照射點應在此入射點稍下的位置上。
電梯裡的人說:我們處於引力場中。由於光沒有質量,它不會受引力場的影響,它會恰好落在入射點正對的點上。
噢!問題出現了。兩個觀察者的意見不一致。然而在電梯裡的人犯了個錯誤。他說光沒有質量,但光有能量,而能量有一個質量(記住一焦耳能量的質量是:M=E/C^2)因此光將有一個向地板彎曲的軌跡,正象外部的觀察者所說的那樣。
由於能量的質量極小(C^2=300,000,000×300,000,000),這種現象只能在非常強的引力場附近被觀察到。這已經被證實:由於太陽的巨大質量,光線在靠近太陽時會發生彎曲。這個試驗是愛因斯坦理論(廣義相對論)的首次實證。
結論
從所有這些實驗中我們得出結論:通過引入一個引力場我們可以把一個加速系視為伽利略系。將其引伸,我們認為它對所有的運動都適用,不論它們是鏇轉的(向心力被解釋為引力場)還是不均勻加速運動(對不滿足黎曼(Riemann)條件的引力場通過數學方法加以轉換)。你看,廣義相對論與實踐處處吻合。
上述例子取自 “L'évolution des idées en Physique” 愛因斯坦和 Leopold Infeld 著。
物理套用
引力透鏡
愛因斯坦十字:同一個天體在引力透鏡效應下的四個成像
 同一個天體在引力透鏡效應下的四個成像
同一個天體在引力透鏡效應下的四個成像引力場中光線的偏折效應是一類新的天文現象的原因。當觀測者與遙遠的觀測天體之間 還存在有一個大質量天體,當觀測天體的質量和相對距離合適時觀測者會看到多個扭曲的天體成像,這種效應被稱作引力透鏡。受系統結構、尺寸和質量分布的影響,成像可以是多個,甚至可以形成被稱作愛因斯坦環的圓環,或者圓環的一部分弧。最早的引力透鏡效應是在1979年發現的,至今已經發現了超過一百個引力透鏡。即使這些成像彼此非常接近以至於無法分辨——這種情形被稱作微引力透鏡——這種效應仍然可通過觀測總光強變化測量到,很多微引力透鏡也已經被發現。
引力波
藝術家的構想圖:雷射空間干涉引力波探測器LISA對脈衝雙星的觀測是間接證實引力波存在的有力證據(參見上文軌道衰減一節)。已經有相當數量的地面引力波探測器投入運行,最著名的是GEO600、LIGO(包括三架雷射干涉引力波探測器)、TAMA300和VIRGO;而美國和歐洲合作的空間雷射干涉探測器LISA正處於開發階段,其先行測試計畫LISA探路者(LISAPathfinder)於2009年底之前正式發射升空。
美國科研人員2016年2月11日宣布,他們利用雷射干涉引力波天文台(LIGO)於去年9月首次探測到引力波。 研究人員宣布,當兩個黑洞於約13億年前碰撞,兩個巨大質量結合所傳送出的擾動,於2015年9月14日抵達地球,被地球上的精密儀器偵測到。證實了愛因斯坦100年前所做的預測。
對引力波的探測將在很大程度上擴展基於電磁波觀測的傳統觀測天文學的視野,人們能夠通過探測到的引力波信號了解到其波源的信息。這些從未被真正了解過的信息可能來自於黑洞、中子星或白矮星等緻密星體,可能來自於某些超新星爆發,甚至可能來自宇宙誕生極早期的暴漲時代的某些烙印,例如假想的宇宙弦。
黑洞和其它
基於廣義相對論理論的計算機模擬一顆恆星坍縮為黑洞並釋放出引力波的過程廣義相對論預言了黑洞的存在,即當一個星體足夠緻密時,其引力使得時空中的一塊區域極端扭曲以至於光都無法逸出。在當前被廣為接受的恆星演化模型中,一般認為大質量恆星演化的最終階段的情形包括1.4倍左右太陽質量的恆星演化為中子星,而數倍至幾十倍太陽質量的恆星演化為恆星質量黑洞。具有幾百萬倍至幾十億倍太陽質量的超大質量黑洞被認為定律性地存在於每個星系的中心,一般認為它們的存在對於星系及更大的宇宙尺度結構的形成具有重要作用。
在天文學上緻密星體的最重要屬性之一是它們能夠極有效率地將引力能量轉換為電磁輻射。恆星質量黑洞或超大質量黑洞對星際氣體和塵埃的吸積過程被認為是某些非常明亮的天體的形成機制,著名且多樣的例子包括星系尺度的活動星系核以及恆星尺度的微類星體。在某些特定場合下吸積過程會在這些天體中激發強度極強的相對論性噴流,這是一種噴射速度可接近光速的且方向性極強的高能等離子束。在對這些現象進行建立模型的過程中廣義相對論都起到了關鍵作用,而實驗觀測也為支持黑洞的存在以及廣義相對論做出的種種預言提供了有力證據。
黑洞也是引力波探測的重要目標之一:黑洞雙星的合併過程可能會輻射出能夠被地球上的探測器接收到的某些最強的引力波信號,並且在雙星合併前的啁啾信號可以被當作一種“標準燭光”從而來推測合併時的距離,並進一步成為在大尺度上探測宇宙膨脹的一種手段。而恆星質量黑洞等小質量緻密星體落入超大質量黑洞的這一過程所輻射的引力波能夠直接並完整地還原超大質量黑洞周圍的時空幾何信息。
宇宙學
威爾金森微波各向異性探測器(WMAP)拍攝的全天微波背景輻射的溫度漲落現代的宇宙模型是基於帶有宇宙常數的愛因斯坦場方程建立的,宇宙常數的值對大尺度的宇宙動力學有著重要影響。
這個經修改的愛因斯坦場方程具有一個各向同性並均勻的解:弗里德曼-勒梅特-羅伯遜-沃爾克度規,在這個解的基礎上物理學家建立了從一百四十億年前熾熱的大爆炸中演化而來的宇宙模型。只要能夠將這個模型中為數不多的幾個參數(例如宇宙的物質平均密度)通過天文觀測加以確定,人們就能從進一步得到的實驗數據檢驗這個模型的正確性。這個模型的很多預言都是成功的,這包括太初核合成時期形成的化學元素初始豐度、宇宙的大尺度結構以及早期的宇宙溫度在今天留下的“回音”:宇宙微波背景輻射。
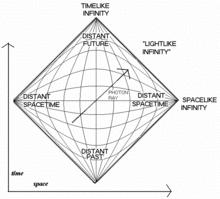 一個無限的靜態閔可夫斯基宇宙的彭羅斯圖
一個無限的靜態閔可夫斯基宇宙的彭羅斯圖從天文學觀測得到的宇宙膨脹速率可以進一步估算出宇宙中存在的物質總量,不過有關宇宙中物質的本性還是一個有待解決的問題。估計宇宙中大約有90%以上的物質都屬於暗物質,它們具有質量(即參與引力相互作用),但不參與電磁相互作用,即它們無法(通過電磁波)直接觀測到。在已知的粒子物理或其他什麼理論的框架中還沒有辦法對這種物質做出令人滿意的描述。另外,對遙遠的超新星紅移的觀測以及對宇宙微波背景輻射的測量顯示,我們的宇宙的演化過程在很大程度上受宇宙常數值的影響,而正是宇宙常數的值決定了宇宙的加速膨脹。換句話說,宇宙的加速膨脹是由具有非通常意義下的狀態方程的某種能量形式決定的,這種能量被稱作暗能量,其本性也仍然不為所知。
在所謂暴漲模型中,宇宙曾在誕生的極早期(~10-33秒)經歷了劇烈的加速膨脹過程。這個在於二十世紀八十年代提出的假說是由於某些令人困惑並且用經典宇宙學無法解釋的觀測結果而提出的,例如宇宙微波背景輻射的高度各向同性,而對微波背景輻射各向異性的觀測結果是支持暴漲模型的證據之一。然而,暴漲的可能的方式也是多樣的,現今的觀測還無法對此作出約束。一個更大的課題是關於極早期宇宙的物理學的,這涉及到發生在暴漲之前的、由經典宇宙學模型預言的大爆炸奇點。對此比較有權威性的意見是這個問題需要由一個完備的量子引力理論來解答,而這個理論至今還沒有建立(參加下文量子引力)。
進階概念
因果結構和全局幾何
一個無限的靜態閔可夫斯基宇宙的彭羅斯圖在廣義相對論中沒有任何有靜止質量的物體能夠追上或超過一束光脈衝,即是說發生於某一點的事件A在光從那一點傳播到空間中任意位置X之前無法對位置X產生影響。因此,一個時空中所有光的世界線(零性測地線)包含了有關這個時空的關鍵因果結構信息。描述這種因果結構的是彭羅斯-卡特圖,在這種圖中無限大的空間區域和時間間隔通過共形變換被“收縮”(數學上稱為緊化)在可被容納的有限時空區域內,而光的世界線仍然和在閔可夫斯基圖中一樣用對角線表示。
彭羅斯和其他研究者注意到因果結構的重要性,從而發展了所謂全局幾何。全局幾何中研究的對象不再是愛因斯坦場方程的一個個特定解(或一族解),而是運用一些對所有測地線都成立的關係,如Raychaudhuri方程,以及對物質本性的非特異性假設(通常用所謂能量條件的形式來表述)來推導普適性結論。
視界
在全局幾何下可以證明有些時空中存在被稱作視界的分界線,它們將時空中的一部分區域隔離起來。這樣的最著名例子是黑洞:當質量被壓縮到空間中的一塊足夠小的區域中後(相關長度為史瓦西半徑),沒有光子能從內部逸出。而由於任何有質量的粒子速度都無法超過光速,黑洞內部的物質也被封閉在視界內。不過,從視界之外到視界之內的通道依然是存在的,這表明黑洞的視界作為一種分界線並不是物理性質的屏障。
一個鏇轉黑洞的能層,在從鏇轉黑洞抽取能量的過程中扮演著重要角色早期的黑洞研究主要依賴於求得愛因斯坦場方程的精確解,著名的解包括球對稱的史瓦西解(用來描述靜態黑洞)和反對稱的克爾解(用來描述鏇轉定態黑洞,並由此引入了能層等有趣的屬性)。而後來的研究通過全局幾何揭示了更多的關於黑洞的普適性質:研究表明經過一段相當長的時間後黑洞都逐漸演化為一類相當簡單的可用十一個參數來確定的星體,包括能量、動量、角動量、某一時刻的位置和所帶電荷。這一性質可歸納為黑洞的唯一性定理:“黑洞沒有毛髮”,即黑洞沒有像人類的不同髮型那樣的不同標記。例如,星體經過引力坍縮形成黑洞的過程非常複雜,但最終形成的黑洞的屬性卻相當簡單。
更值得一提的是黑洞研究已經得到了一組制約黑洞行為的一般性定律,這被稱作黑洞(熱)力學,這些定律與熱力學定律有很強的類比關係。例如根據黑洞力學的第二定律,一個黑洞的視界面積永不會自發地隨著時間而減少,這類似於一個熱力學系統的熵;這個定律也決定了通過經典方法(例如,彭羅斯過程)不可能從一個鏇轉黑洞中無限度地抽取能量。這些都強烈暗示了黑洞力學定律實際是熱力學定律的一個子集,而黑洞的表面積和它的熵成正比。從這個假設可以進一步修正黑洞力學定律。例如,由於黑洞力學第二定律是熱力學第二定律的一部分,則可知黑洞的表面積也有可能減小,只要有某種其它過程來保證系統的總熵是增加的。而熱力學第三定律認為不存在溫度為絕對零度的物體,可以進一步推知黑洞應該也存在熱輻射;半經典理論計算表明它們確實存在有熱輻射,在這個機制中黑洞的表面引力充當著普朗克黑體輻射定律中溫度的角色,這種輻射稱作霍金輻射(參見下文量子理論一節)。
廣義相對論還預言了其他類型的視界模型:在一個膨脹宇宙中,觀察者可能會發現過去的某些區域不能被觀測(所謂“粒子視界”),而未來的某些區域不能被影響(事件視界)。即使是在平直的閔可夫斯基時空中,當觀察者處於一個加速的參考系時也會存在視界,這些視界也會伴隨有半經典理論中的盎魯輻射。
奇點
廣義相對論的另一個普遍卻又令人困擾的特色問題是時空的分界線——奇點的出現。時空可以通過沿著類時和類光的測地線來探索,這些路徑是光子及其他所有粒子在自由落體運動中的可能軌跡,但愛因斯坦場方程的某些解具有“粗糙的邊緣”——這被稱作時空奇點,這些奇點上類時或類光的測地線會突然中止,而對於這些奇點沒有定義好的時空幾何來描述。需要說明的是,“奇點”往往可能並不是一個“點”:那些場方程的解的“粗糙邊緣”在既有坐標系下,不僅可能是一個“點”,還可以以其他幾何形式出現(比如克爾黑洞的“奇環”等)。一般意義上的奇點是指曲率奇點,這是說在這些點上描述時空曲率的幾何量,例如里奇張量為無限大(曲率奇點是相對所謂坐標奇點而言的,坐標奇點本質上不屬於奇點的範疇:有些度規在某個特定坐標下會產生無窮大,但本質上這些點不具有奇性,在其他合適的坐標下是光滑的,也不會產生無窮大的曲率張量)。描述未來的奇點(世界線的終結)的著名例子包括永遠靜態的史瓦西黑洞內部的奇點,以及永遠鏇轉的克爾黑洞內部的環狀奇點。弗里德曼-勒梅特-羅伯遜-沃爾克度規,以及其他描述宇宙的時空幾何都具有過去的奇點(世界線的開端),這被稱作大爆炸奇點,而有些還具有未來的奇點(大擠壓)。
考慮到這些模型都是高度對稱從而被簡化的,人們很容易去猜測奇點的出現是否只是理想狀態下的不自然產物。然而著名的由全局幾何證明的奇點定理指出,奇點是廣義相對論的一個普遍特色結果,並且任何有質量的實體發生引力坍縮並達到一個特定階段後都會形成奇點,而在一系列膨脹宇宙模型中也一樣存在奇點。不過奇點定理的內容基本沒有涉及到奇點的性質,這些關於確定奇點的一般結構(例如所謂BKL假說)的問題是當前相關研究的主要課題。另一方面,由於在對於物理規律的破壞方面而言,一個被包裹於視界之中的奇點被認為要好過一個“裸”的奇點,故而宇宙監督假說被提出,它認為所有未來的實際奇點(即沒有完美對稱性的具有實際性質的物體形成的奇點)都會被藏在視界之內,從而對外面對觀察者不可見,即自然界憎恨裸奇點。儘管還沒有實際證據證明這一點,有數值模擬的結果支持這一假說的正確性。
演化方程
每一個愛因斯坦場方程的解都是一個宇宙,這裡的宇宙含義既包括了整個空間,也包括了過去與未來——它們並不單單是反映某些事物的“快照”,而是所描述的時空的完全寫真。每一個解在其專屬的特定宇宙中都能描述任意時間和任意位置的時空幾何和物質狀態。出於這個表征,愛因斯坦的理論看上去與其他大多數物理理論有所不同:大多數物理理論都需要指明一個物理系統的演化方程(例如量子力學中的埃倫費斯特定理),即如果一個物理系統在給定時刻的狀態已知,其演化方程能夠允許描述系統在過去和未來的狀態。愛因斯坦理論中的引力場和其他場的更多區別還在於前者是自身相互作用的(是指它在沒有其他場出現時仍然還是非線性的),並且不具有固定的背景結構(在宇宙尺度上會發生演化)。
為了更好地理解愛因斯坦場方程這個與時間有關的偏微分方程,可以將它寫成某種能夠描述宇宙隨時間演化的形式。這種形式被稱作“3+1”分解,其中時空被分為三維空間和一維時間。最著名的形式叫做ADM形式,在這種分解下廣義相對論的時空演化方程具有良好的性質:在適當的初始條件給定的情形下方程有解並且是唯一的。場方程的“3+1”分解形式是數值相對論的研究基礎。
全局和準局部量
演化方程的觀念與廣義相對論性物理中的另一個方面緊密聯繫:在愛因斯坦的理論中,一個系統的總質量(或能量)這個看似簡單的概念無法找到一種普遍性的定義。其原因在於,引力場原則上並不像其他的場那樣具有可以局部化的能量。
儘管如此,試圖通過其他途徑來定義一個系統的總質量還是可能的,在經典物理中,質量(或能量)的定義可以來自時間平移不變性的守恆量,或是通過系統的哈密頓形式。在廣義相對論中,從這兩種途徑出發可以分別得到如下質量的定義:
* 柯瑪質量:從類時的Killing矢量出發通過柯瑪積分得到的在時間平移不變性下的守恆量,表現為一個靜態時空的總能量;
* ADM質量:在一個漸近平直時空中建立廣義相對論的哈密頓形式,從中定義系統的總能量。
如果將一個系統的總質量中被引力波攜帶至無限遠處的能量除去,得到的結果叫做零性無限遠處的邦迪質量。這些定義而來的質量被舍恩和丘成桐的正質量定理證明是正值,而動量和角動量也具有全局的相應定義。在這方面的研究中還有很多試圖建立所謂準局部量的嘗試,例如僅通過一個孤立系統所在的有限空間區域中包含的物理量來構造這個孤立系統的質量。這類嘗試寄希望於能夠找到一個更好地描述孤立系統的量化方式,例如環假說的某種更精確的形式。
量子理論
如果說廣義相對論是現代物理學的兩大支柱之一,那么量子理論作為我們藉此了解基本粒子以及凝聚態物理的基礎理論就是現代物理的另一支柱。然而,如何將量子理論中的概念套用到廣義相對論的框架中仍然是一個未能解決的問題。
量子場論
作為現代物理中粒子物理學的基礎,通常意義上的量子場論是建立在平直的閔可夫斯基時空中的,這對於處在像地球這樣的弱引力場中的微觀粒子的描述而言是一個非常好的近似。而在某些情形中,引力場的強度足以影響到其中的量子化的物質但不足以要求引力場本身也被量子化,為此物理學家發展了彎曲時空中的量子場論。這些理論藉助於經典的廣義相對論來描述彎曲的背景時空,並定義了廣義化的彎曲時空中的量子場理論。通過這種理論,可以證明黑洞也在通過黑體輻射釋放出粒子,這即是霍金輻射,並有可能通過這種機制導致黑洞最終蒸發。如前文所述,霍金輻射在黑洞熱力學的研究中起到了關鍵作用。
量子引力
物質的量子化描述和時空的幾何化描述之間彼此不具有相容性,以及廣義相對論中時空曲率無限大(意味著其結構成為微觀尺度)的奇點的出現,這些都要求著一個完整的量子引力理論的建立。這個理論需要能夠對黑洞內部以及極早期宇宙的情形做出充分的描述,而其中的引力和相關的時空幾何需要用量子化的語言來敘述。儘管物理學家為此做出了很多努力,並有多個有潛質的候選理論已經發展起來,至今人類還沒能得到一個稱得上完整並自洽的量子引力理論。
一個卡拉比-丘流形的投影,由弦理論所提出的緊化額外維度的一種方法量子場論作為粒子物理的基礎已經能夠描述除引力外的其餘三種基本相互作用,但試圖將引力概括到量子場論的框架中的嘗試卻遇到了嚴重的問題。在低能區域這種嘗試取得了成功,其結果是一個可被接受的引力的有效(量子)場理論,但在高能區域得到的模型是發散的(不可重整化)。
圈量子引力中的一個簡單自鏇網路
試圖克服這些限制的嘗試性理論之一是弦論,在這種量子理論中研究的最基本單位不再是點狀粒子,而是一維的弦。弦論有可能成為能夠描述所有粒子和包括引力在內的基本相互作用的大統一理論,其代價是導致了在三維空間的基礎上生成六維的額外維度等反常特性。在所謂第二次超弦理論革新中,人們猜測超弦理論,以及廣義相對論與超對稱的統一即所謂超引力,能夠構成一個猜想的十一維模型的一部分,這種模型叫做M理論,它被認為能夠建立一個具有唯一性定義且自洽的量子引力理論。
另外一種嘗試來自於量子理論中的正則量子化方法。套用廣義相對論的初值形式(參見上文演化方程一節),其結果是惠勒-得衛特方程(其作用類似於薛丁格方程)。雖然這個方程在一般情形下定義並不完備,但在所謂阿西特卡變數的引入下,從這個方程能夠得到一個很有前途的模型:圈量子引力。在這個理論中空間是一種被稱作自鏇網路的網狀結構,並在離散的時間中演化。
當前進展
在引力和宇宙學的研究中,廣義相對論已經成為了一個高度成功的模型,至今為止已經通過了每一次意義明確的觀測和實驗的檢驗。然而即便如此,仍然有證據顯示這個理論並不是那么完善的:對量子引力的尋求以及時空奇點的現實性問題依然有待解決;實驗觀測得到的支持暗物質和暗能量存在的數據結果也在暗暗呼喚著一種新物理學的建立;而從先驅者號觀測到的反常效應也許可以用已知的理論來解釋,也許則真的是一種新物理學來臨的預告。不過,廣義相對論之中仍然充滿了值得探索的可能性:數學相對論學家正在尋求理解奇點的本性,以及愛因斯坦場方程的基本屬性;不斷更新的計算機正在進行黑洞合併等更多的數值模擬;廣義相對論最後一個預言(引力波)已被證實,人類探測到了引力波,對宇宙的認識將會到達一個新的領域。在愛因斯坦發表他的理論九十多年之後,廣義相對論依然是一個高度活躍的研究領域。
基礎教案
廣義相對性原理和等效原理狹義相對論認為,在不同的慣性參考系中一切物理規律都是相同的.愛因斯坦在此基礎上又向前邁進了一大步,認為在任何參考系中(包括非慣性系)物理規律都是相同的,這就是廣義相對性原理.
下面介紹廣義相對論的另一個基本原理-等效原理.
等效原理
假設宇宙飛船是全封閉的,太空人和外界沒有任何聯繫,那么他就沒有任何辦法來判斷,使物體以某一加速度下落的力到底是引力還是慣性力.實際上,不僅是自由落體的實驗,飛船內部的任何物理過程都不能告訴我們,飛船到底是在加速運動,還是停泊在一個行星的表面.這裡談到的情景和本章第一節所述伽利略大船中的情景十分相似.這個事實使我們想到:一個均勻的引力場與一個做勻加速運動的參考系等價.愛因斯坦把它作為廣義相對論的第二個基本原理,這就是著名的等效原理.
從這兩個基本原理出發可以直接得出一些意想不到的結論.假設在引力可以忽略的宇宙空間有一艘宇宙飛船在做勻加速直線運動,一束光垂直於運動方向射入這艘飛船.船外靜止的觀察者當然會看到這束光是沿直線傳播的,但是飛船中的觀察者以飛船為參考系看到的卻是另外一番情景.為了記錄光束在飛船中的徑跡,他在船中等距離地放置一些半透明的屏(如圖),光可以透過這些屏,同時在屏上留下光點.由於飛船在前進,光到達下一屏的位置總會比到達上一展的位置更加靠近船尾.如果飛船做勻速直線運動,光在任何相鄰兩屏之間飛行時,飛船前進的距離都相等,飛船上的觀察者看到光的徑跡仍是一條直線(如圖中的虛線),儘管直線的方向與船外靜止觀察者看到的直線方向不一樣.如果飛船做勻加速直線運動,在光向右傳播的同時,飛船的速度也在不斷增大,因此船上觀察者記錄下的光的徑跡是一條拋物線(如圖中的實線).
根據等效原理,飛船中的觀察者也完全可以認為飛船沒有加速運動,而是在船尾方向存在一塊巨大的物體,它的引力場影響了飛船內的物理過程.因此我們得出結論:物體的引力能使光線彎曲.
通常物體的引力場都太弱,20世紀初只能觀測到太陽引力場引起的光線彎曲.由於太陽引力場的作用,我們有可能看到太陽後面的恆星(如圖).但是,平時的明亮天空使我們無法觀星,所以最好的時機是發生日全食的時候.1919年5月29日恰好有一次日全食,兩支英國考察隊分赴幾內亞灣和巴西進行觀測,其結果完全證實了愛因斯坦的預言.這是廣義相對論的最早的驗證.
 廣義相對論
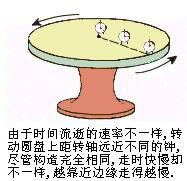
廣義相對論時間間隔與引力場有關 引力場的存在使得空間不同位置的時間進程出現差別. 我們考察一個轉動的巨大圓盤(如圖).從地面上看,圓盤上除轉動軸的位置外,各點都在做加速運動,越是靠近邊緣,加速度越大,方向指向盤心.從地面上還會看到,越是靠近邊緣的點,速度越大.根據狹義相對論,同一個過程,越是發生在靠近邊緣的位置,這個過程所持續的時間就越長.或者說,靠近邊緣位置的時間進程比較緩慢.
再以圓盤本身為參考系研究這個現象.圓盤上的人認為,盤上存在著一個引力場,方向由盤心指向邊緣.既然靠近邊緣位置的時間進程比較緩慢,盤上的人就可以得出結論:在引力勢較低的位置,時間進程比較慢.
宇宙中有一類恆星,體積很小,質量卻不小,叫做矮星.矮星表面的引力很強,引力勢比地球表面低得多.矮星表面的時間進程比較慢,那裡的原子發光的頻率比同種原子在地球上發光的頻率低,看起來偏紅.這個現象叫做引力紅移,已經在天文觀測中得到證實.現代技術也能夠在地球上驗證引力紅移.
桿的長度與引力場有關 仍然考察轉動的圓盤.同樣的桿,放在盤上的不同位置,它們隨盤運動的速度就不一樣,根據狹義相對論,它們的長度也就不一樣,越是靠近邊緣,桿就越短.盤上的人也觀察到了這種差別,不過他以圓盤為參考系,認為盤是靜止的,同時他還認為盤上各點存在著指向圓盤邊緣的引力,因此他得出結論:引力勢越低的位置,桿的長度越短.
桿的長度和引力場的分布有關,這個現象反映出這樣的事實,即由於物質的存在,實際空間並不是均勻的,這和我們過去的觀念有很大的差別.打個比方,一塊布上面的格子是整齊的(如圖甲),如果用手向下壓,格子就彎曲了(如圖乙).物理學借用了“彎曲”這個詞,通常說,由於物質的存在,實際的空間是彎曲的.
行星沿橢圓軌道繞太陽運動,有時離太陽近些,有時遠些.太陽的巨大質量使它周圍的空間發生彎曲,其結果是,行星每公轉一周它的軌道的長軸都比上一個周期偏轉一個角度,這個現象叫做行星軌道的進動.理論分析表明只有水星軌道的進動比較顯著,達到約每世紀0.01°.這個現象早在廣義相對論出現之前就已經發現,只是無法解釋,所以它實際是廣義相對論的最早的佐證.
廣義相對論與幾何學最後,我們再次回到轉動的圓盤.狹義相對論告訴我們,只有沿著運動方向的長度發生變化,垂直於運動方向的長度不會變化;如果以圓盤為參考系,就可以說,沿著引力方向的空間尺度沒有變化,只有垂直於引力方向的空間尺度發生了改變.這一點具有非常深刻的意義,因為這時測量圓盤的周長和直徑,它們的比值就不再是3.141 59…,而是別的值,三角形的內角和也不會是180°了……簡而言之,由於實際空間是彎曲的,我們學習的幾何學已經不適用了.
幾何學反映的是人對空間關係的認識.有史以來人們只是在比較小的空間尺度中接觸到比較弱的引力場.這種情況下空間的彎曲可以忽略,在此基礎上人類發展了歐幾里得幾何學,它反映了平直空間的實際.廣義相對論告訴我們實際空間是彎曲的,因此描述實際空間的應該是更具有一般意義的非歐幾何.不過,作為非歐幾何的特例,歐幾里得幾何學在它的適用範圍內仍是正確的,還將繼續發揮作用.
1905年愛因斯坦發表狹義相對論後,他開始著眼於如何將引力納入狹義相對論框架的思考。以一個處在自由落體狀態的觀察者的理想實驗為出發點,他從1907年開始了長達八年的對引力的相對性理論的探索。在歷經多次彎路和錯誤之後,他於1915年11月在普魯士科學院上作了發言,其內容正是著名的愛因斯坦引力場方程。這個方程描述了處於時空中的物質是如何影響其周圍的時空幾何,並成為了愛因斯坦的廣義相對論的核心[1]。
愛因斯坦的引力場方程是一個二階非線性偏微分方程組,數學上想要求得方程的解是一件非常困難的事。愛因斯坦運用了很多近似方法,從引力場方程得出了很多最初的預言。不過很快天才的天體物理學家卡爾·史瓦西就在1916年得到了引力場方程的第一個非平庸精確解——史瓦西度規,這個解是研究星體引力坍縮的最終階段,即黑洞的理論基礎。在同一年,將史瓦西幾何擴展到帶有電荷的質量的研究工作也開始進行,其最終結果就是雷斯勒-諾斯特朗姆度規,其對應的是帶電荷的靜態黑洞[2]。1917年愛因斯坦將廣義相對論理論套用於整個宇宙,開創了相對論宇宙學的研究領域。考慮到同時期的宇宙學研究中靜態宇宙的學說仍被廣為接受,愛因斯坦在他的引力場方程中添加了一個新的常數,這被稱作宇宙常數項,以求得和當時的“觀測”相符合[3]。然而到了1929年,哈勃等人的觀測表明我們的宇宙處在膨脹狀態,而相應的膨脹宇宙解早在1922年就已經由亞歷山大·弗里德曼從他的弗里德曼方程(同樣由愛因斯坦場方程推出)得到,這個膨脹宇宙解不需要任何附加的宇宙常數項。比利時牧師勒梅特套用這些解構造了宇宙大爆炸的最早模型,模型預言宇宙是從一個高溫高緻密狀態演化來的[4]。愛因斯坦其後承認添加宇宙常數項是他一生中犯下的最大錯誤[5]。
在那個時代,廣義相對論與其他物理理論相比仍保持了一種神秘感。由於它和狹義相對論相融洽,並能夠解釋很多牛頓引力無法解釋的現象,顯然它要優於牛頓理論。愛因斯坦本人在1915年證明了廣義相對論是如何解釋水星軌道的反常近日點進動的現象,其過程不需要任何附加參數(所謂“敷衍因子”)[6]。另一個著名的實驗驗證是由亞瑟·愛丁頓爵士率領的探險隊在非洲的普林西比島觀測到的日食時的光線在太陽引力場中的偏折[7],其偏折角度和廣義相對論的預言完全相符(是牛頓理論預言的偏折角的兩倍),這一發現隨後被全球報紙競相報導,一時間使愛因斯坦的理論名聲赫赫[8]。但是直到1960年至1975年間,廣義相對論才真正進入了理論物理和天體物理主流研究的視野,這一時期被稱作廣義相對論的黃金時代。物理學家逐漸理解了黑洞的概念,並能夠通過天體物理學的性質從類星體中識別黑洞[9]。在太陽系內能夠進行的更精確的廣義相對論的實驗驗證進一步展示了廣義相對論非凡的預言能力[10],而相對論宇宙學的預言也同樣經受住了實驗觀測的檢驗[11]。