簡史
1957年：基於剛球勢的分子動力學法（AlderandWainwright）
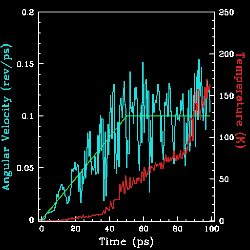分子動力學1964年：質點系への拡張(Rahman)
1971年：剛體系への拡張(RahmanandStillinger)
1977年：約束動力學方法（Rychaert等）
1980年：恆壓條件下的動力學方法（Andersenの方法、Parrinello-Rahman法）
1983年：非平衡態動力學方法(GillanandDixon)
1984年：恆溫條件下的動力學方法（能勢‐フーバーの方法）
1985年：第一原理分子動力學法（→カー・パリネロ法）
1991年：巨正則系綜的分子動力學方法(CaginandPettit)
基本步驟
確定起始構型
分子動力學進行分子動力學模擬的第一步是確定起始構型，一個能量較低的起始構型是進行分子模擬的基礎，一般分子的起始構型主要來自實驗數據或量子化學計算。
在確定起始構型之後要賦予構成分子的各個原子速度，這一速度是根據波爾茲曼分布隨機生成的，由於速度的分布符合波爾茲曼統計，因此在這個階段，體系的溫度是恆定的。另外，在隨機生成各個原子的運動速度之後須進行調整，使得體系總體在各個方向上的動量之和為零，即保證體系沒有平動位移。
進入平衡相
由上一步確定的分子組建平衡相，在構建平衡相的時候會對構型、溫度等參數加以監控。
進入生產相
進入生產相之後體系中的分子和分子中的原子開始根據初始速度運動，可以想像其間會發生吸引、排斥乃至碰
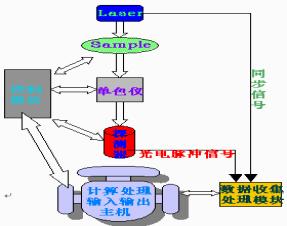分子動力學計算結果
用抽樣所得體系的各個狀態計算當時體系的勢能，進而計算構型積分。
作用勢與動力學計算
作用勢的選擇與動力學計算的關係極為密切，選擇不同的作用勢，體系的勢能面會有不同的形狀，動力學計算所
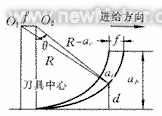分子動力學時間步長與約束動力學
分子動力學計算的基本思想是賦予分子體系初始運動狀態之後利用分子的自然運動在相空間中抽取樣本進行統計
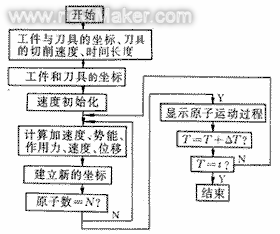分子動力學但是通常情況下，體系各自由度中運動周期最短的是各個化學鍵的振動，而這種運動對計算某些巨觀性質並不產生影響，因此就產生了禁止分子內部振動或其他無關運動的約束動力學，約束動力學可以有效地增長分子動力學模擬的時間步長，提高搜尋相空間的能力。
套用
分子動力學可以用於NPT，NVE，NVT等系綜的計算，是一種基於牛頓力學確定論的熱力學計算方法，與蒙特卡洛
分子動力學另外，在實際套用中，經常把分子動力學方法和蒙特卡羅法聯合使用。
模擬簡述
分子動力學計算機模擬是研究複雜的凝聚態系統的有力工具。這一技術既能得到原子的運動軌跡,還能象做實驗一樣作各種觀察。對於平衡系統,可以在一個分子動力學觀察時間(observationtime)內作時間平均來計算一個物理量的統計平均值,對於一個非平衡系統過程,只要發生在一個分子
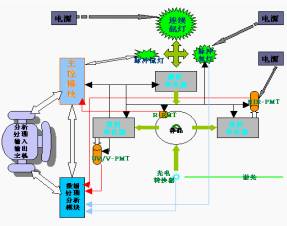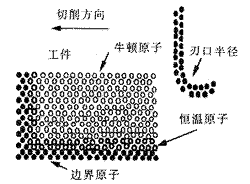分子動力學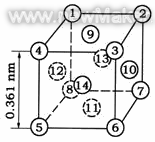
分子動力學
分子動力學另外經驗勢近似有一個本身的局限性,它丟失了局域電子結構之間存在著的強相關作用信息,也就是說,不能得到成鍵性質(bondingproperties),以及原子動力學過程中的電子性質。儘管在某些特殊情況下,電子性質也能通過經驗勢近似來得到,例如用經驗勢的分子動力學來計算原子結構時,選取某幾種原子構型來作電子結構計算,這樣不僅耗時,而且原子動力學和電子結構計算成了相互獨立的過程。1985年,Car和Parrinello在傳統的分子動力學中引入了電子的虛擬動力學,把電子和核的自由度作統一的考慮,首次把密度泛函理論與分子動力學有機地結合起來,提出了從頭計算分子動力學方法(也稱CP方法),使基於局域密度泛函理論的第一原理計算直接用於統計力學模擬成為可能,極大地擴展了計算機模擬實驗的廣度和深度。
參見
計算化學分子模擬en:moleculardynamicsja:分子動力學法nl:Moleculairedynamica
物理學知識2
| 物理學(PHYSICS)是研究物質世界最基本的結構、最普遍的相互作用、最一般的運動規律及所使用的實驗手段和思維方法的自然科學，簡稱物理。物理學是人們對無生命自然界中物質的轉變的知識做出規律性的總結。 |
