巨正則系綜
正文
組成系綜的系統與一溫度為T、化學勢為μ的很大的熱源、粒子源相接觸,此時系統不僅同熱源有能量交換,而且可以同粒子源有粒子的交換,最後達到平衡,這種系綜稱巨正則系綜。也可以這樣構想:取M(M是一很大的數)個體積為V的相同的系統構成系綜,其中任意一個系統均可作為所研究的系統, 其餘M-1個系統起著恆溫槽和粒子源的作用,系統間既有能量交換,又有粒子交流,並共同處於平衡,但各個系統在空間的位置不同,因而它們是可以分辨的。巨正則系綜的分布公式為
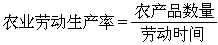 ,
,
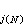 的微觀態j上的幾率。式中Ξ 叫做巨配分函式,可表示為
的微觀態j上的幾率。式中Ξ 叫做巨配分函式,可表示為 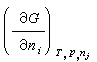 ,
,
巨正則分布的經典表示式為
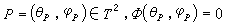
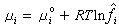
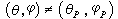 =Ξ
=Ξ -1exp【(-
-1exp【(-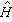 +μ
+μ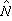 )/kT】,
)/kT】,
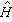 和
和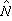 分別是系統的哈密頓算符和粒子數算符。而巨配分函式可表為
分別是系統的哈密頓算符和粒子數算符。而巨配分函式可表為 Ξ(T,V,μ)=tr{exp【(-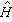 +μ
+μ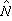 )/kT】},
)/kT】},
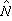 的本徵值求和。
的本徵值求和。 巨配分函式Ξ 是平衡態統計物理中一個非常重要的量,它不是算符,而是溫度、體積和化學勢的函式,其重要性在於它同系統的熱力學量如能量、壓強、粒子數平均值、熵、巨熱力勢等有直接的聯繫,只要求出Ξ ,就可得到系統所有的平衡態熱力學量。在巨正則系綜中,系統在某時刻的能量和粒子數同它們的平均值間存在著偏差,即漲落,其大小用相對漲落來量度。能量的相對漲落是