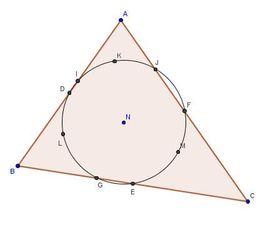
定義
任意三角形三條高線的垂足、三邊中點以及頂點與垂心的三條連線的中點,共九點都在半徑為1/2R(三角形外接圓半徑)的圓上,且圓心是外心與垂心所連線段的中點。這個圓稱為九點圓,這是龐斯萊命名的。
歷史
數學家歐拉在1765年就發現了九點圓,因此人們稱之為“歐拉圓”。這是幾何學中很著名的問題,在18世紀與19世紀之交已廣為流傳。1804年英國的培亞敏俾凡在雷榜《算理之庫》卷一第十八章中,正式提出“九點”問題,布德衛斯與韋唐給出了證明。1821年格蓋尼和1822年彭色列先後正式發表這一問題。1822年德國人費爾巴哈在《直角三角形的一些特殊點的性質》里,發表了自己的證法,並且說九點圓與內切圓及三個旁切圓相切。這就是人們通常所稱的“費爾巴哈定理”。1827年維茲在《哲學雜誌》發表一篇論文,對九點圓進行了比較詳細的論述。
證明
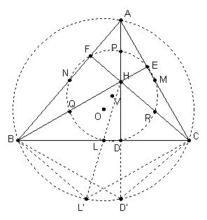 九點圓
九點圓如右圖所示,△ABC的BC邊垂足為D,BC邊中點為L。證法為以垂心H為位似中心,1/2為位似比作位似變換。
連結HL並延長至L',使LL'=HL;做H關於BC的對稱點D'。
顯然,∠BHC=∠FHE=180°-∠A,所以∠BD'C=∠BHC=180°-∠A,從而A,B,D',C四點共圓。
又因為BC和HL'互相平分於L,所以四邊形BL'CH為平行四邊形。故∠BL'C=∠BHC=180°-∠A,從而A,B,L',C四點共圓。
綜上,A,B,C,D',L'五點共圓。顯然,對於另外兩邊AB,AC邊上的F,N,E,M也有同樣的結論成立,故A,B,C,D',L',F',N',E',M'九點共圓。此圓即△ABC的外接圓⊙O。
接下來做位似變換,做法是所有的點(⊙O上的九個點和點O本身)都以H為位似中心進行位似比為1/2的位似變換。那么,L'變到了L(因為HL'=2HL),D'變到了D(因為D'是H關於BC的對稱點),B變到了Q,C變到了R(即垂心與頂點連線的中點)。其它各點也類似變換。O點變成了OH中點V。
位似變換將圓仍映射為圓(容易用向量證明),因此原來在⊙O上的九個點變成了在⊙V上的九個點,且⊙V的半徑是⊙O的一半。
這就證明了三角形三邊的中點,三高的垂足和三個歐拉點都在一個圓上。
性質
九點圓具有許多有趣的性質,例如:
1. 三角形的九點圓的半徑是三角形的外接圓半徑之半;
2. 九點圓的圓心在歐拉線上,且恰為垂心與外心連線的中點;
3. 三角形的九點圓與三角形的內切圓,三個旁切圓均相切(費爾巴哈定理);
4. 九點圓是一個垂心組(即一個三角形三個頂點和它的垂心,共四個點,每個點都是其它三點組成的三角形的垂心,共4個三角形)共有的九點圓,所以九點圓共與四個內切圓、十二個旁切圓相切。
5. 九點圓心(V),重心(G),垂心(H),外心(O)四點共線,且HG=2OG,OG=2VG,OH=2OV。