定理定義
密克定理是幾何學中關於相交圓的定理。1838年,奧古斯特·密克(Auguste Miquel)敘述並證明了數條相關定理。許多有用的定理可由其推出。
定理陳述
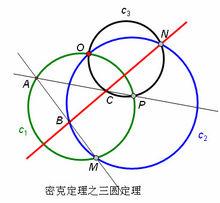
三圓定理:設三個圓C1, C2, C3交於一點O,而M, N, P分別是C1 和C2, C2和C3, C3和C1的另一交點。設A為C1的點,直線MA交C2於B,直線PA交C3於C。那么B, N, C這三點共線。(注意:M、N、P並不共線)
 密克定理
密克定理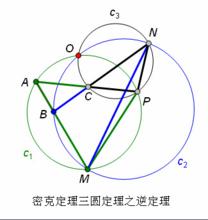 密克定理
密克定理證明思路:
1、圓C2和C3用圓冪定理,再套到C1里,化簡得梅涅勞斯等式。
2、連幾條線,三個四點共圓導角得到三點共線。(三圓共點的條件可以轉換成三條公共弦的三線共點)
3、先畫兩個圓,假設點N是BC延長線與圓c2的交點,再導角證明OCPN共圓
逆定理:如果是三角形,M, N, P三點分別在邊AB, BC, CA上,那么△AMP、△BMN、△CPN 的外接圓交於一點O。
完全四線形定理
如果ABCDEF是完全四邊形,那么三角形的外接圓交於一點 O,稱為密克點。
四圓定理
 密克定理
密克定理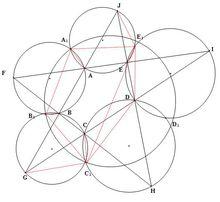 密克定理
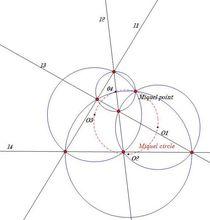
密克定理設C1, C2,C3, C4為四個圓,A1和B1是C1和C2的交點,A2和B2是C2 和C3的交點,A3和B3是C3和C4的交點,A4和B4是C1和C4的交點。那么A1, A2, A3, A4四點共圓若且唯若B1, B2, B3, B4四點共圓。
五圓定理
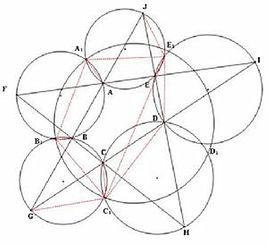
設ABCDE為任意五邊形,五點F, G, H, I, J分別是EA和BC , AB和CD, BC和DE, CD和EA, DE和AB的交點,那么三角形的外接圓的五個不在五邊形上的交點共圓, 不穿過這些交點的圓也穿過五個外接圓的圓心。
發展簡史
1838年奧古斯特·密克在約瑟夫·劉維爾的期刊《Journal de mathématiques pures et appliquées》(純粹與套用數學雜誌)發表了這定理的一部份。
密克的第一條定理,是十八世紀已有的著名經典結果,以圓周角定理證明。
完全四線形四圓的交點稱為密克點,但這性質雅各布·施泰納在1828年已經知道,威廉·華萊士也已經知道。
五圓定理是一條更一般的定理的特殊情形。這條定理由威廉·金登·克利福德提出及證明。2000年12月20日,江澤民主席出席澳門回歸祖國一周年慶典活動期間,在參觀濠江中學時向該校師生出了一道求證“五點共圓”的問題,令問題重新引起廣泛興趣。阿蘭·科納在2002年10月的一個研討會也重提這問題。