三角級數
形如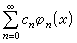
的級數稱為正交函數級數，其中сn是和x無關的實數,{φn(x)}是在某固定區間【α,b】上正交的函式系,特別當正交函式系是【0,2π】上的三角函式系時，相應的級數可寫作 
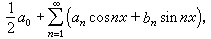(1)
三角級數三角級數(1)還可以寫成下面複數形式的級數：
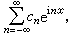(2)
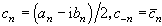（叿n表示сn的共軛複數）。級數(2)的部分和Sn理解為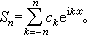
如果三角級數(1)對一切實數x都收斂,那么(1)表示了實數軸上的一個周期為2π周期函式ƒ(x),即ƒ(x+2π)=ƒ(x)對一切x∈(- ∞，∞)都成立。這是因為(1)中每一項都是周期為2π的周期函式。但是實際問題往往是，對給定的函式ƒ，如果它是具有周期2π的周期函式,需要把它表示成三角級數(1)。19世紀初,法國科學家J.-B.-J.傅立葉在研究熱的流動時，為了求解熱方程，首先就提出了這個想法。他的構想，雖然從現在的觀點看，缺乏理論的嚴謹性，但卻是人們對三角級數進行研究的出發點，對於近代數學以及物理、工程等許多學科都有著深遠的影響。
如果三角級數(1)一致收斂於連續函式ƒ(x),那么用coskx或sinkx去乘級數(1)，再在區間(0,2π)上進行積分，注意到逐項積分的可能性，就得到係數αn,bn與函式ƒ的關係式：
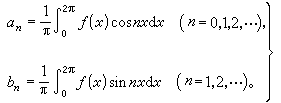(3)
對於給定的周期函式ƒ(x)，如果ƒ是可積的,那么從(3)式仍然可以得到αn，bn，從而得到相應的傅立葉級數(1)。這就建議人們去研究ƒ 的傅立葉級數是否收斂於ƒ以及有關的許多問題。從19世紀到現在,傅立葉級數的理論逐步得到建立，已成為三角級數理論中的一個基礎分支，也是一個具有廣泛套用的工具學科（見傅立葉級數）。
傅立葉級數的性質，由函式ƒ可以通過(3)進行研究。自然要問，任意的三角級數(1),是否為某函式的傅立葉級數呢？這個問題的答案是否定的。因為根據傅立葉係數的性質，傅立葉係數αn,bn必須滿足條件
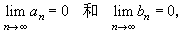
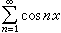是三角級數，而不是傅立葉級數。 那么係數αn,bn趨於0的三角級數(1),是否為傅立葉級數呢?下面的例子
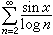說明,它的係數趨於0，而且級數處處收斂於某函式ƒ(x)，但因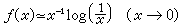 
三角級數(1)的共軛級數是
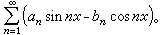(4)
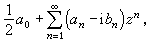(5)
值得注意的是，傅立葉級數的共軛級數未必是傅立葉級數。例如，級數
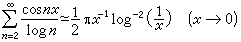
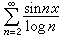卻不是傅立葉級數。但是可以證明，如果級數(1)是某函式ƒ的傅立葉級數，並且|ƒ|p 是可積的，其中p>1,那么它的共軛級數(4)也是傅立葉級數。 一般的三角級數,由於不存在關係式(3)，因此增加了它的複雜性。到目前為止，人們對它的了解還是十分初步的。值得注意的是，三角級數往往可以提供許多奇特的函式，這對數學理論的基礎研究，有著重大的意義。
例如，用所謂F.里斯的無窮乘積
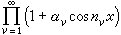(6)
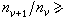
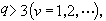且係數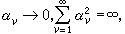
那么(6)乘得的三角級數幾乎處處收斂於0，而它的係數卻不全為0。 又例如缺項很多的三角級數
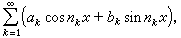(7)
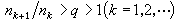時，稱為阿達馬缺項三角級數。它具有很奇特的性質：要么幾乎處處收斂於一個平方可積函式,要么幾乎處處不收斂,如屬後者，則它不是傅立葉級數。 中國在三角級數方面開展研究最早的是陳建功。他從1928年開始就在日本《東京皇家科學院學報》發表關於正交函式級數的文章，他於1930年在日本岩波書店出版的《三角級數論》是國際上三角級數論方面較早的專著之一。
