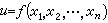多元微積分學
正文
關於多元函式的微積分學,是微積分學的一個組成部分。它是體現在一元函式的微分學和積分學中的基本概念和計算方法在套用到多元函式的情形的發展。在這發展中,基本概念都被推廣到多元的情形,而計算方法則被化歸到一元的情形。從而計算仍舊是在實數範圍內進行。這樣,多元微積分學的基本任務便在於,以一元微積分學為基礎,來闡述其中基本概念和計算的規律對於任意多個變數的函式仍然一致有效,同時分析由於變數個數的增多而帶來的特點。把一元函式的研究擴展到多元函式
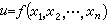 的這兩個基本任務,都在n=2的情形中便已表現出了它們的一般性;所以主要就二元函式u=ƒ(x,y)進行敘述,只是在進一步展示新的特點有需要時才考慮n=3的情形。
的這兩個基本任務,都在n=2的情形中便已表現出了它們的一般性;所以主要就二元函式u=ƒ(x,y)進行敘述,只是在進一步展示新的特點有需要時才考慮n=3的情形。 多元微分學 一元函式微分學到多元函式的擴展。
連續性 設在同一個過程中,變數u隨著變數x和y而變化,就稱u為x和y的一個函式,記為
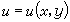 。
。
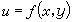 。
。
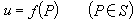 。 (1)
。 (1)
如圖1
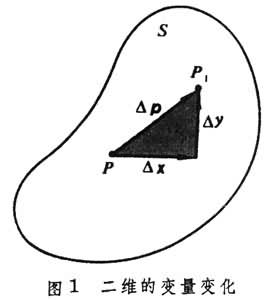 ,當動點P由一個位置 P(x,y)變到另一個位置P1(x1y1)時,這變化由它的位移向量
,當動點P由一個位置 P(x,y)變到另一個位置P1(x1y1)時,這變化由它的位移向量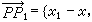
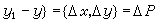 來刻畫,這變化的大小便由這向量的長度
來刻畫,這變化的大小便由這向量的長度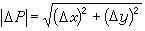 來度量。相應的u的變化
來度量。相應的u的變化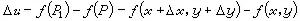 ,其大小由|Δu|來度量。於是多元函式(1)在一點P 處的連續性也同一元函式的一致,即在P1無限趨近於P的過程中,|Δu|隨著|ΔP|而無限變小。這就是說,對於每一個正數ε都存在一個正數δ使得
,其大小由|Δu|來度量。於是多元函式(1)在一點P 處的連續性也同一元函式的一致,即在P1無限趨近於P的過程中,|Δu|隨著|ΔP|而無限變小。這就是說,對於每一個正數ε都存在一個正數δ使得  。 (2)
。 (2)
函式(1)的連續性,作為一個局部性質,它在S的每個內點處都可以分解成一元的情形。如圖2
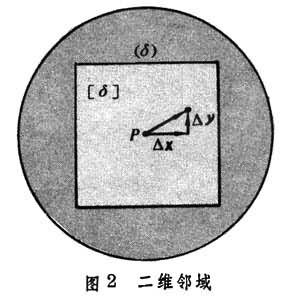 ,只要函式(1)在一點P的某個領域(δ)內處處連續,則(根據上述基本性質)必定在其內部的一個方鄰域 【δ】上一致連續,而在這個方鄰域上的變化量具有圖1所啟示的向量分解式
,只要函式(1)在一點P的某個領域(δ)內處處連續,則(根據上述基本性質)必定在其內部的一個方鄰域 【δ】上一致連續,而在這個方鄰域上的變化量具有圖1所啟示的向量分解式 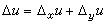 , (3)
, (3)
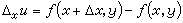 ,
,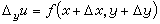
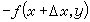 分別作為一元函式
分別作為一元函式 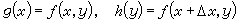 (4)
(4)
偏導數 連續性(2)的進一步研究,是要在變化量分解式(3)的基礎上,利用一元函式(4)來闡明,在|ΔP|趨向0的過程中,變化量Δu隨 Δx、Δy趨向0的依賴關係。這就要用到一元函式(4)的變化率,即導數g
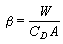 (x)、h
(x)、h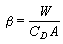 (y)。假定它們在P(x,y)的附近都存在,並分別記為ƒ
(y)。假定它們在P(x,y)的附近都存在,並分別記為ƒ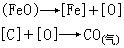 (x,y)。ƒ
(x,y)。ƒ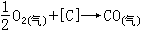 (x+Δx,y)通常也寫成
(x+Δx,y)通常也寫成 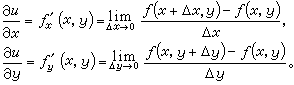
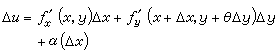 ,
,
 連續時,可以進一步寫成
連續時,可以進一步寫成 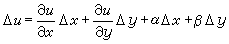 , (5)
, (5)
全微分 分解式(5)表明,在點P 處,變化量 Δu隨著Δx、Δy 趨向0的過程中,存在著近似線性的依賴關係
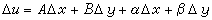 , (6)
, (6)
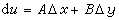 。 (7)
。 (7)
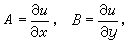
不過,公式(6)的推導已經表明,這些偏導數的連續性可以保證微分存在。這時就說函式是連續可微的。最基本的連續可微函式就是自變數本身作為 P=(x,y)的函式:
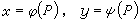 。 (8)
。 (8)
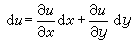 。 (9)
。 (9)
變數替換 在微分形式(9)中,變數x、y既然當作動點P的函式,如(8)所示,它們也就是動點P在任一別的坐標系(r,s)中的坐標的函式:
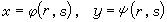 。 (10)
。 (10)
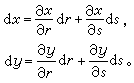 (11)
(11)
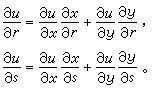 (12)
(12)
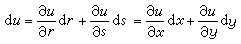 。
。
變數替換(10)規定了一個坐標平面上的動點P(x,y)隨著另一坐標平面上的動點Q(r,s)而變動,因而定義了一個函式T:P=T(Q)。這樣,函式組(10)便被表示成一個函式。它經過微分轉化成的線性(微分)方程組(11)可以縮寫成一個矩陣方程
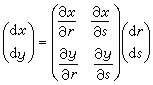 。
。
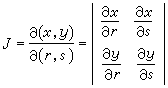 。 (13)
。 (13)
如果(8)中的動點 P是在一個三維坐標空間(r,s,t)中,則(10)中的函式應是三元的:
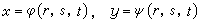 。
。
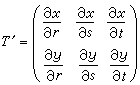 (14)
(14)
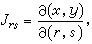
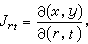
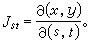
多元積分學 一元函式積分學到多元函式的擴展。
重積分 一元函式的定積分,作為黎曼積分和的極限,推廣到二元函式(1)幾乎是直接的。這裡,積分區間,作為自變數的變化範圍,換成了兩個區間X(α≤x≤A)和Y(b≤y≤B),它們的乘積R=X×Y是包含有界閉區域S的(各邊平行於坐標軸的)最小的矩形(圖3
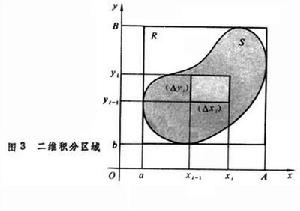 )。對於R上不屬於S的點,取函式值為0,並仿照一元的情形作黎曼和數
)。對於R上不屬於S的點,取函式值為0,並仿照一元的情形作黎曼和數 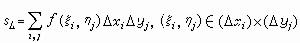 。
。
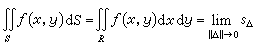 。
。
在可積的前提下,二重積分可以寫成
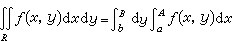 , (15)
, (15)
面積微分dR=dxdy,作為一個微小矩形的面積,在坐標變換(10)之下由這變換的微分形式(11)來確定,成為一個以向量
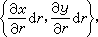 和
和 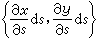 為一對鄰邊的平行四邊形的面積,即行列式
為一對鄰邊的平行四邊形的面積,即行列式 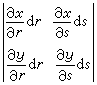
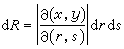 。
。
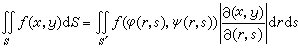 。 (16)
。 (16)
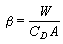 =(α≤r≤A)×(b≤s≤B)上的連續可微的函式,而以(r,s)作為P的一種新的坐標(曲面坐標)。這裡 S
=(α≤r≤A)×(b≤s≤B)上的連續可微的函式,而以(r,s)作為P的一種新的坐標(曲面坐標)。這裡 S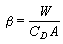 的微小矩形(Δr)×(Δs)對應著 S上的微小曲面四邊形 ΔS,後者的面積關於前者的面積 ΔrΔs 的線性主要部分便是曲面的面積微分dS。它等於以切線向量
的微小矩形(Δr)×(Δs)對應著 S上的微小曲面四邊形 ΔS,後者的面積關於前者的面積 ΔrΔs 的線性主要部分便是曲面的面積微分dS。它等於以切線向量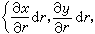
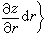 和
和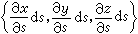 為一對鄰邊的平行四邊形的面積:
為一對鄰邊的平行四邊形的面積: 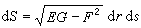 ,
,
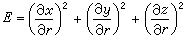 ,
, 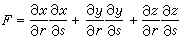 。
。 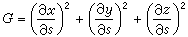 。
。
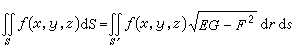 。 (17)
。 (17)
線積分 如果我們類似地考慮空間中一條光滑的(或逐段光滑的)曲線C上關於弧長的微分ds的積分
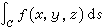 ,
,
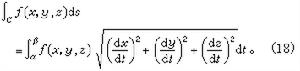
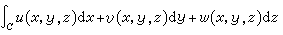 ,
,
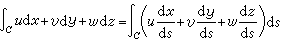 , (19)
, (19)
公式(15)~(19)表明,定積分在概念上的各種推廣,在計算上仍都能回到定積分。
基本公式 定積分,作為微分之逆,到各種積分的推廣,導致這互逆關係的基本公式(牛頓-萊布尼茨公式)的推廣。這公式的意義在於,函式的導數經過積分運算之後,便消去導數中所含的微分運算而返回到原來函式的差分,起著化簡的作用。我們現在先考慮嬠w/嬠z,積分區域取為一個橢球體V。用R 表示V 在 xy平面上的垂直投影,S1和 S0表示上下邊
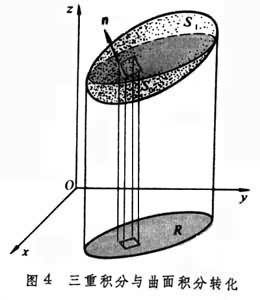 界面,S 表示全部邊界面,
界面,S 表示全部邊界面,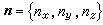 表示其單位外法向量(圖4)。如果這偏導數在V 上處處存在並且可積,則其三重積分可以像二重積分(15)那樣分解,然後通過牛頓-萊布尼茨公式轉化為邊界S上的曲面積分:
表示其單位外法向量(圖4)。如果這偏導數在V 上處處存在並且可積,則其三重積分可以像二重積分(15)那樣分解,然後通過牛頓-萊布尼茨公式轉化為邊界S上的曲面積分: 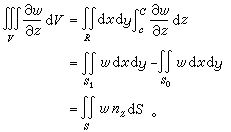
奧斯特羅格拉茨基公式:
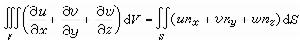 , (20)
, (20)
取V=S0×(0,1),u=u(x,y),υ =υ(x,y),w=0,這公式就化成二維空間中的奧氏公式:
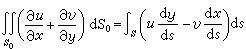 , (21)
, (21)
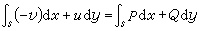 ,
,
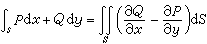 , (22)
, (22)
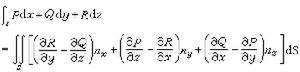 (23)
(23)
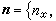
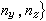 在組成S的每一光滑片段上是隨起點(x,y,z)而連續變動的,它到這片區域的外法向量、再到邊界曲線的切線向量所構成的螺鏇轉向同正z軸到正x軸、再到正y軸的螺鏇轉向是一致的,並且任何相鄰兩片段的定向在邊界曲線的公共部分上是相反(相消)的。
在組成S的每一光滑片段上是隨起點(x,y,z)而連續變動的,它到這片區域的外法向量、再到邊界曲線的切線向量所構成的螺鏇轉向同正z軸到正x軸、再到正y軸的螺鏇轉向是一致的,並且任何相鄰兩片段的定向在邊界曲線的公共部分上是相反(相消)的。 由這個公式推知,在開區域V內,若要一個帶連續係數的微分式Pdx+Qdy+Rdz恰好是某一函式的全微分,就必須它的係數滿足恆等式
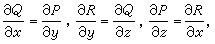
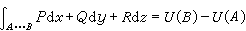 (24)
(24)
歷史上,多元微積分學的基本概念都是在微分與積分的基本思想的套用中,與一元函式的合為一體,適應描述和分析物理現象和規律的需要而產生的。偏導數、重積分的樸素思想(I.牛頓,1687),二重積分及其累次積分與換元計算方法(L.歐拉,1769),三重積分及其累次積分與換元計算方法(J.-L.拉格朗日,1773)都是初期出現在力學研究的著作中,並不是有意識地要建立相關的數學理論。牛頓-萊布尼茨公式的兩種形式(20)和(21)都延遲了一個時期才明確出現在熱傳導和電磁的研究中(M.B.奧斯特羅格拉茨基,1828;G.格林,1828),且是作為物理定理來理解的。變數替換中的雅可比行列式也延遲到微積分的理論分析開展起來以後,才獲得明確的概念和系統的研究(C.G.J.雅可比1833、1841,奧斯特羅格拉茨基1834),而變數替換中隱含著的曲線坐標則同時延遲到熱傳導和電磁的研究中問題求解的需要和物理意義的啟示達到相當明朗的程度,才獲得明確的概念和系統的研究(G.拉梅1833、1859)。只有斯托克斯公式是作為格林公式的理論套用來敘述的(L.開爾文,1850;G.G.斯托克斯,1854)。不過這時微積分學已由於它的理論分析的發展而成為一門自立的學科了。
總的說來,多元微積分學是在微積分的基本思想的套用和發展中自然地、水到渠成般地形成起來的。