簡介
已知平面上兩點A,B,則所有滿足PA/PB=k且不等於1的點P的軌跡是一個圓,這個軌跡最先由古希臘數學家阿波羅尼斯發現,故稱阿氏圓。解答
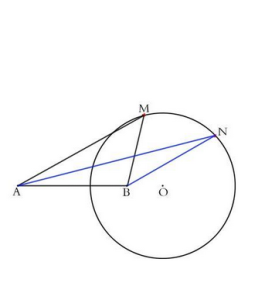 阿波羅尼斯圓
阿波羅尼斯圓而PA=根號;(x-a)^2+y^2;
PB=根號;x^2+y^2;
整理得(1-k^2)(x^2+y^2)-2ax+a^2=0;
當k不為1時,它的圖形是圓。
當k為1時,軌跡是兩點的中垂線。
阿氏圓又稱阿波羅尼斯圓,已知平面上兩點A,B,則所有滿足PA/PB=k且不等於1的點P的軌跡是一個圓,這個軌跡最先由古希臘數學家阿波羅尼斯發現,具體的描述:一動點P到兩定點A、B的距離之比等於定比m:n,則P點的軌跡,是以定比m:n內分和外分定線段AB的兩個分點的連線為直徑的圓。該圓稱為阿波羅尼斯圓,簡稱阿氏圓。
 阿波羅尼斯圓
阿波羅尼斯圓而PA=根號;(x-a)^2+y^2;
PB=根號;x^2+y^2;
整理得(1-k^2)(x^2+y^2)-2ax+a^2=0;
當k不為1時,它的圖形是圓。
當k為1時,軌跡是兩點的中垂線。
阿氏貝喙鯨,是大型的喙鯨類,阿氏貝喙鯨在南半球大致呈環極區分布,由南極洲浮冰邊緣往北達約南緯34度,大多數都在南緯40度以南的地方,最常在塔斯曼海一帶發...
概述 形態特徵 分布區域 生活習性 生長繁殖阿史那(Ashina) 為古突厥統治家族的姓氏,意為 “高貴的狼”,也具有“藍色” 之意,阿史那部因此被稱為 “藍突厥”,藍色並不是指有藍色的眼睛,而是...
突厥 突厥國史 歷代君主 文獻記載王氏,今河南北部的衛輝一帶.不僅廣泛分布於全國各地,還走出了國門,走向了世界。從東南亞至歐美,都可有王氏人物的活動足跡。
近現代王姓家族地域分布 王氏來源 王氏簡介石霜楚圓這樣一位在宋代禪宗史上有著深遠影響的禪師,學術界對他的事跡、禪法思想作專題研究或整理的成果,目前尚未見到。只是在宋代禪宗或宋代佛教史的研究專著或...
簡介 生平 開悟 傳承 地位飛魚科為輻鰭魚綱鶴鱵目的其中一科。
信息 主要分布 形態特徵: 棲所生態:阿氏沼澤鷦鷯是一種小型鳴禽,身長13厘米。分布於南美洲,棲息地僅限於接近塘和沼澤地的蘆葦叢。
外形特徵 分布範圍 生活習性 生長繁殖 亞種分布圓瑛法師(1878-1953):中國近代佛教領袖,1929年與太虛共同發起成立中國佛教會,並連續數屆當選主席,法師一生為團結全國佛教徒、促進和平作出了巨...
人物生平 出家事件 弘法思想 佛學思想 主要著作圓瑛法師(1878-1953):中國近代佛教領袖,1929年與太虛共同發起成立中國佛教會,並連續數屆當選主席,法師一生為團結全國佛教徒、促進和平作出了巨...
人物生平 出家事件 弘法思想 佛學思想 主要著作