內容
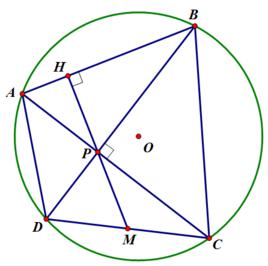
在圓內接四邊形ABCD中，AC⊥BD,自對角線的交點P向一邊作垂線，其延長線必平分對邊。 （又譯"卜拉美古塔定理"）這個定理有另一個名稱,叫做"婆羅摩笈多定理"
證明
證法一
設PH⊥CD,PM交AB於M.
顯然AP/BP=DP/CP,故AM=BM←AP*sin∠APM=BP*sin∠BPM←DP*sin∠PDH=CP*sin∠PCD←PH=PH,證畢
證法二
以下為向量式
設BF=xAF 則EF=（EB+xEA）/(1+x) （定比分點向量公式）
又EF*BC=EF*(DE+EC)=0
所以（EB+xEA)(DE+EC)=0
拆開 EB*DE+EB*EC+xEA*DE+xEA*EC=0
由垂直 所以只有 EB*DE+xEA*EC=0
由相交線定理 所以x=1（EA*EC=EB*ED)（這是代數式，上式為向量式，故成立）
證法三
證明：（向量式）
EF=1/2(EA+EB)
DC=DE+EC
EF*DC=0（去掉垂直的）
證法四
再給出一個用歐幾里得幾何方法的初等證明：
由∠PDC+∠ACD=90°,∠PDC+∠HPD=90°推出∠ACD=∠HPD推出∠ABD=∠MPB①推出BM=PM②
由∠ABD+∠BAC=90°及①推出∠BAC+∠MPB=90°③
由∠MPA+∠MPB=90°及③推出∠BAC=∠MPA推出AM=PM④
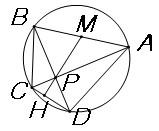布拉美古塔定理聯②④即得AM=BM
推廣
推廣過圓內接四邊形兩對角線交點作任一邊的垂線，必過以其對邊為一邊，以交點為頂點的三角形的外心。
