定義
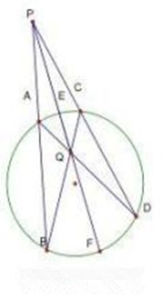
 割線定理
割線定理從圓外一點L引兩條割線與圓分別交於A.B.C.D則有LA·LB=LC·LD=LT^2。如右圖所示。(LT是切線)
割線定理為圓冪定理之一,其他兩條定理為:
切割線定理
相交弦定理
證明
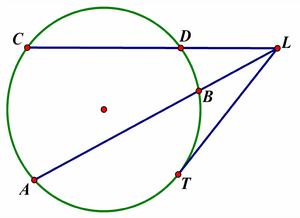
 證明一
證明一一.如圖直線ABP和CDP是自點P引的⊙O的兩條割線,則PA·PB=PC·PD
證明:連線AD、BC∵∠A和∠C都對弧BD
∴由圓周角定理,得∠A=∠C
又∵∠APD=∠CPB
∴△ADP∽△CBP
∴AP:CP=DP:BP,也就是AP·BP=CP·DP
二、既然圓內接四邊形定理可以從割線定理而得,那么或許割線定理就可以從圓內接四邊形定理而得。
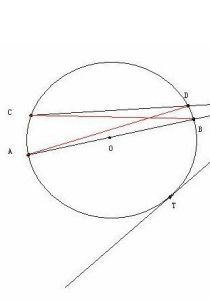
如圖所示。
已知:從圓O外一點P引兩條圓的割線,一條交圓於A、B,另一條交圓於C、D
求證:AP·BP=CP·DP
證明:連線AC、BD
由圓內接四邊形定理得
∠ABD+∠DCA=∠CAB+∠BDC=180°
又∵∠ACP+∠DCA=∠DCP=180°,∠CAP+∠CAB=∠BAP=180°(平角的定義)
∴∠ABD=∠ACP,∠BDC=∠CAP(同角的補角相等)
∴△ACP∽△DBP(兩角對應相等的三角形相似)
∴AP/DP=CP/BP(相似三角形對應邊成比例)
∴AP·BP=CP·DP(比例基本性質)
三、根據切割線定理求證。
已知:從圓O外一點P引兩條圓的割線,一條交圓於A、B,另一條交圓於C、D
求證:AP·BP=CP·DP
過點P作圓O的切線,記切點為T
由切割線定理可知:AP·BP=PT^2,CP·DP=PT^2
所以AP·BP=CP·DP
比較
割線定理與相交弦定理,切割線定理統稱為圓冪定理。