中垂線

基本信息

• 中文名：中垂線

• 又稱：垂直平分線
• 所屬領域：幾何
• 巧計方法：點到線段兩端的距離相等
• 所屬學科：數學
• 相關定理：中垂線定理

概念

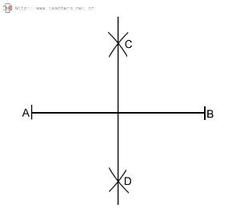
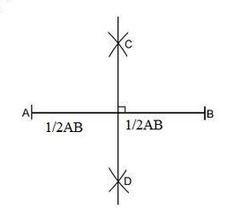中垂線

垂直於一條線段並且平分這條線段的直線，叫做這條線段的中垂線。

性質

1.中垂線垂直且平分其所在線段。2.中垂線上任意一點，到線段兩端點的距離相等。

性質定理

線段垂直平分線上的點到這條線段的兩個端點的距離相等。（逆定理）到一條線段兩個端點距離相等的點，在這條線段的垂直平分線上。

證明方法

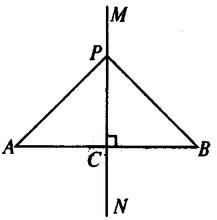中垂線

可以通過全等三角形證明。到一條線段兩個端點距離相等的點，在這條線段的垂直平分線上。如圖：直線MN即為線段AB的垂直平分線。注意：要證明一條直線為一條線段的垂直平分線，應滿足兩個點到這條線段的兩個端點的距離相等且這兩個點都在要求證明的直線上才可以證明。通常來說，垂直平分線會與全等三角形聯合使用。逆定理到一條線段兩個端點距離相等的點，在這條線段的垂直平分線上。

作圖方法

1：尺規作圖法（主要方法、考試考點）2：度量法3：摺紙法（摺疊法）

判定

①利用定義：經過某一條線段的中點，並且垂直於這條線段的直線是線段的垂直平分線。
②到一條線段兩個端點距離相等的點，在這條線段的垂直平分線上．（即線段垂直平分線可以看成到線段兩端點距離相等的點的集合）。

尺規作法

方法一

線上段的中心找到這條線段的中點通過這個點做這條線段的垂線段。

方法二

1、分別以線段的兩個端點為圓心，以大於線段的二分之一長度為半徑畫弧線。得到兩個交點(兩交點交於線段的兩側)。2、連線這兩個交點。原理：等腰三角形的高垂直平分底邊。

方法三

利用等腰三角形的性質：1、三線合一(等腰三角形底邊上的高、底邊上的中線、頂角的平分線相互重合。)2、等角對等邊（如果一個三角形，有兩個內角相等，那么它一定有兩條邊相等。）3、等邊對等角（在同一三角形中,如果兩條邊相等,則兩個邊的對角相等,即等邊對等角。

方法四

軸對稱圖形。