定理介紹
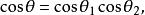最小角定理
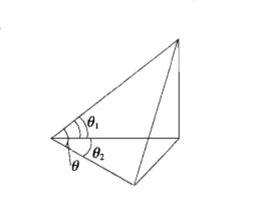
最小角定理平面外的一條斜線和它在平面內的射影所成的銳角，是這條斜線和平面內經過斜足的直線所成的一切角中最小的角 。（為最小角，如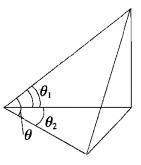圖1）。
圖1定理證明
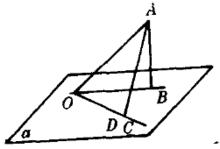圖2如圖，若AB，AO分別是平面a的垂線和斜線，OB是AO在平面a內的射影，∠AOB為銳角，OC是平面a內和OB不重合的任一直線，在OC上截取OD=OB，連結AD，則AB<AD。
在△AOB與△AOD中，因為OA=OA，OB=OD，AB<AD，所以∠AOB<∠AOD。
定理得證。
上述定理是定義“斜線和平面所成的角”這一概念的理論基礎。有了上面的性質，就保證了這一概念的定義的合理性 。
例題解析
【例1】直線AB與直二面角α-a-β的兩個面分別交於A、B兩點，且A、B都不在棱a上，設直線AB與平面α和平面β所成的角分別為θ和中，求θ+φ的取值範圍。
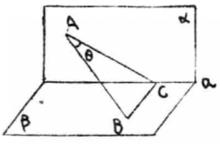圖3解：如圖3，作BC⊥a於C，
∵平面α⊥平面β，
∴BC⊥平面α。
∴∠BAC是AB與平面α所成的角。
即∠BAC=θ。
又從BC⊥平面α可知BC⊥AC。
在Rt△BAC中：θ+∠ABC=90°。
由最小角定理可知:φ≤∠ABC，
∴θ+φ≤90°。
故θ+φ∈(0°，90°] 。
