譜綜合
正文
又稱調和綜合，是一個與譜分析(或稱調和分析)相對立的概念，它是調和分析與代數的理想理論中一個具有非常綜合性的研究課題。譜分析與譜綜合的原始含義如下：設ƒ(x)是一個周期振動的量,它可用圓周群T上的函式來描述，實驗指出這樣的振動往往由一個基頻及其整數倍頻的簡諧振動疊加而成,定出ƒ的簡諧振動分量的過程稱為譜分析。熟知的傅立葉展開便是這一過程，ƒ的傅立葉係數不為0的點集稱為ƒ的譜集。相反的過程是由ƒ的分量複合出ƒ自己，這個過程就叫譜綜合。對ƒ∈lp(T),1≤p≤∞，各種各樣的傅立葉級數求和法便實現了譜綜合。因此從其原始含義說來，譜綜合與譜分析都不是很複雜的概念。但現在所謂的譜綜合已經演變成一個既概括又抽象，並且很有發展前途的研究課題。
通常所說的譜綜合是研究局部緊交換群G上，l∞(G)中哪些元素可以由它的譜經過某種方法“綜合”出來；或者等價地說是指研究l1(G)的哪些閉理想能被G的對偶群弿中的一個閉子集完全決定。
關於l∞(G)的譜綜合 這裡l∞(G)不是指所有本性有界函式的集合賦極大模的空間,而是同一集合賦弱*拓撲的空間。先對g∈l∞定義譜集的概念。粗略而言,g的譜集就是抭（表示傅立葉變換）的支集。更確切一些的定義是：設F是l∞(G)的閉平移不變子空間，既然弿是由G上有界函式構成的，則弿 ∩F有意義,記它為∑(F),並稱之為F的譜集。對任意g∈l∞(G)，記【g】為由g生成的閉平移不變子空間,簡記∑(【g】)為∑(g),並稱它為g的譜集。如果g能被∑(g)中的元素的線性組合逼近，則每個h∈【g】亦然。這時,集合∑(g)(它是弿 中一個閉集)完全決定了l∞(G)中的閉平移不變子空間【g】。所謂l∞(G)的譜綜合便是研究l∞(G)的哪些閉平移不變子空間可被弿的一個閉集完全決定。它的一個特殊情形是研究怎樣的g∈l∞(G)能被∑(g)中元素的線性組合逼近。可以證明如果l∞(G)中g的傅立葉變換是函式或測度,則上面定義的譜集∑(g)就是g的傅立葉變換的支集。這種情況下,譜集與譜綜合概念就回到了它們的原始理解。
關於l1(G)的譜綜合 設 I是l1(G)的任意一個閉理想，令
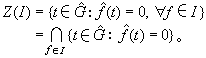(1)
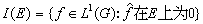
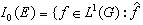在E的一個鄰域上為0}-(“-”表示閉包)也是以 E為傅立葉變換的公共零點集的閉理想,並且I(E)是最大的，I0(E)是最小的。l1(G)的譜綜合也可以說是研究對怎樣的E有I(E)＝I0(E)。滿足這個性質的E稱為譜綜合集。如果所有閉集E嶅弿 都是譜綜合集，則稱l1(G)的譜綜合成立。 l∞(G)與l1(G)的譜綜合的等價 可以證明對任意閉集E嶅弿，存在惟一閉理想I嶅l1(G)使Z(I)=E,若且唯若存在惟一閉平移不變子空間F嶅l∞(G)使∑(F)=E。這就是說，l∞(G)與l1(G)的譜綜合是等價的。
譜綜合的已知重要結果 對所有緊群G,譜綜合是成立的。但對非緊群G,情況要複雜得多。40年代末期，L.施瓦爾茨第一個舉例說明l1(R 3)的譜綜合不成立，他指出R 3中單位球面不是譜綜合集。約10年後，P.馬利阿溫一般地證明了l1(G)的譜綜合當G非緊時是不成立的。
C.H.赫茨舉出了Rn中譜綜合集的許多例子，V.A.迪特金給出了弿 中閉集是譜綜合集的充分條件。作為這個充分條件的推論,得知l1(G)中除了自己以外不可能有別的閉理想使其傅立葉變換無公共零點(概括而言此即"空集是譜綜合集")。值得提出的是，這個推論包含了著名的 N.維納的陶伯定理：如果φ ∈l∞(G),ƒ∈l1(G)滿足弮(t)≠0，對一切任意t∈弿，並且
， (2)
∈l1(G)，當用g代替ƒ時，式(2)仍成立。此外,沿著l∞(G)的譜綜合方向,A.博靈有一系列的工作。例如，他指出對非零的g∈l∞(G)，∑(g)是非空的。這正是“空集是譜綜合集”的另一種說法。 譜綜合的其他等價提法和推廣 譜綜合還有一個常見的等價提法是用擬測度的語言。l∞(G)的傅立葉變換的集合記為PM(弿),其中的元素就稱為弿上的擬測度。l1(G)的傅立葉變換的集合
A(弿 )是一個巴拿赫代數，作為一個巴拿赫空間,其對偶空間正是由PM(弿)的元素構成的。因此可以在PM(弿)中賦弱*拓撲。譜綜合的另一種提法就是研究怎樣的S∈PM(弿)可以被由S的支集中的點支撐的點測度的線合組合弱*逼近。這種提法實際上是使用傅立葉變換將l∞(G)的譜綜合的提法的改裝。類似地,也可用傅立葉變換概念將l1(G)的譜綜合提法改裝。l1(G)的譜綜合提法還可推廣到對任意正則交換巴拿赫代數 A。對這樣的A的譜綜合是研究A的怎樣的閉理想I可以被A的極大理想空間X的一個閉集完全決定；這等價於說,怎樣的I可以表為正規極大理想的交（式(1)最右邊的表示便是正規極大理想的交）；也等價於說，怎樣的I使得 I=ker(hull(I))；
也等價於說X的怎樣的閉集是A的惟一理想的蓋爾范德變換的公共零點集。參考書目
C.C.Graham and O.C.McGehee,Essays in Commuta-tive harmonic Analysis,Springer-Verlag,New York, 1979.
E.Hewitt and K.R.Ross,Abstract harmonic ɑnalysis,Vol.1～2,Springer-Verlag,Berlin,1963, 1970.
