群上調和分析
正文
又稱群上傅立葉分析、抽象調和分析。它是古典調和分析(即傅立葉級數與傅立葉積分理論)的統一與推廣。它的研究對象是拓撲群上的函式或測度以及由它們構成的空間或代數。概論 在古典調和分析中,為了研究一個實變數的函式(即實軸群R上的函式)或周期函式(即圓周群T上的函式),傅立葉提倡的方法是將此函式ƒ按三角函式系
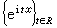 或
或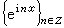 展開。這就要先求出ƒ的傅立葉變換弮(t),t∈R 或傅立葉係數
展開。這就要先求出ƒ的傅立葉變換弮(t),t∈R 或傅立葉係數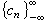 ,式中
,式中 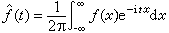 ,
,
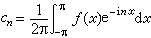 , (1)
, (1)
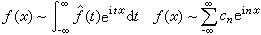 。 (2)
。 (2)
古典調和分析的兩個方面(即級數部分與積分部分)無論就結果與方法而言都十分相似。此外,還發現沃爾什級數與傅立葉級數相似,梅林變換與傅立葉變換相似。這些相似使人們容易想到它們之間或許存在某種本質上相同的東西。把式(1)中兩式合併寫成
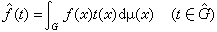 , (1)┡
, (1)┡
 ,dμ(x)兩種情況下都表示勒貝格測度dx。可以發現兩種情況下G都是群;弿是由G決定的另一個群;t(x)是復值函式,它的值域在複平面的單位圓周上,並且滿足乘性關係:t(x·y)=t(x)t(y)(式中·表示群的運算);而dμ(x)是群G上一個有特殊地位的測度。除了傅立葉係數與變換可以這樣統一以外,沃爾什係數與梅林變換也能用上述式 (1)┡表示。對前者只需令G=【0,1】,並在G中定義一個按位模2加法使之成為二進群D;弿=Z+;
,dμ(x)兩種情況下都表示勒貝格測度dx。可以發現兩種情況下G都是群;弿是由G決定的另一個群;t(x)是復值函式,它的值域在複平面的單位圓周上,並且滿足乘性關係:t(x·y)=t(x)t(y)(式中·表示群的運算);而dμ(x)是群G上一個有特殊地位的測度。除了傅立葉係數與變換可以這樣統一以外,沃爾什係數與梅林變換也能用上述式 (1)┡表示。對前者只需令G=【0,1】,並在G中定義一個按位模2加法使之成為二進群D;弿=Z+;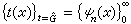 (式中{ψn(x)}是沃爾什函式系,按佩利次序排列);dμ就是勒貝格測度。對後者只需令G=R+(正實數的乘法群);弿=R;
(式中{ψn(x)}是沃爾什函式系,按佩利次序排列);dμ就是勒貝格測度。對後者只需令G=R+(正實數的乘法群);弿=R; 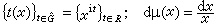 。
。
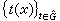 (式(2)說明
(式(2)說明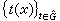 能複合出許多函式,象積木能複合出許多建築物一樣)?20世紀20年代中期,(C.H.)H.外爾先對某些特殊緊李群,然後與F.彼得合作對一般緊李群得到了上述幾個問題的滿意回答,建立了著名的外爾-彼得定理,從而奠定了緊群上調和分析的基礎。其後不久,A.哈爾對滿足某些條件的局部緊群證明了第一個問題中的特殊測度(通稱哈爾測度)的存在性。A.韋伊在其後的幾年,對局部緊群上的哈爾測度及局部緊交換群上的調和分析進行了一系列的奠基研究,並於1940年發表名著《拓撲群上的積分及其套用》,從而宣告了這一學科的誕生。除此以外以И.М.蓋爾范德為首的蘇聯學派對群上調和分析的形成與發展也作了十分關鍵的貢獻。由於對既不是交換也不是緊的一般拓撲群,上述第二、三兩個問題甚至都不能說已經有了令人滿意的答案,因此這方面的調和分析仍處於待發展階段。但若對群附加別的限制條件,如李群結構,則此時的 弿與
能複合出許多函式,象積木能複合出許多建築物一樣)?20世紀20年代中期,(C.H.)H.外爾先對某些特殊緊李群,然後與F.彼得合作對一般緊李群得到了上述幾個問題的滿意回答,建立了著名的外爾-彼得定理,從而奠定了緊群上調和分析的基礎。其後不久,A.哈爾對滿足某些條件的局部緊群證明了第一個問題中的特殊測度(通稱哈爾測度)的存在性。A.韋伊在其後的幾年,對局部緊群上的哈爾測度及局部緊交換群上的調和分析進行了一系列的奠基研究,並於1940年發表名著《拓撲群上的積分及其套用》,從而宣告了這一學科的誕生。除此以外以И.М.蓋爾范德為首的蘇聯學派對群上調和分析的形成與發展也作了十分關鍵的貢獻。由於對既不是交換也不是緊的一般拓撲群,上述第二、三兩個問題甚至都不能說已經有了令人滿意的答案,因此這方面的調和分析仍處於待發展階段。但若對群附加別的限制條件,如李群結構,則此時的 弿與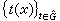 有比較滿意的選擇,並且在某些特殊情形下,它們還能被具體地寫出來。這樣,古典調和分析中的某些定量結果也能推廣到這種情形。
有比較滿意的選擇,並且在某些特殊情形下,它們還能被具體地寫出來。這樣,古典調和分析中的某些定量結果也能推廣到這種情形。 群論觀點進入調和分析除了有上述統一與推廣的意義外,還使某些看起來彼此不相關的現象間的內在聯繫被揭示得更清楚,這使得調和分析內部各分支之間以及調和分析與其他學科例如泛函分析、代數學、群表示論、模形式等的聯繫變得更為密切。因此,群上調和分析可以說是一門既具套用價值(正如它對機率論、數論與微分方程等所起的作用所說明的)又具理論意義的綜合性學科。
局部緊T2群 一個既有群結構(其群運算用乘法表示)又有拓撲結構,並且兩者有某種聯繫的集合稱為一個拓撲群。當它的拓撲結構是局部緊的並且滿足T2分離性時就稱為局部緊T2群。群上調和分析主要只考慮這樣的群。
哈爾測度 局部緊群 G上的在左(右)平移作用下不變的非負(不恆為0)正規波萊爾測度稱為G的左(右)哈爾測度。所謂“平移作用下的不變測度”的含意可以有兩種等價理解。設μ是G上一個測度。對每個α∈G都可定義G上的一個左平移x→αx,凬x∈G,相應地每個μ可測集E被平移為αE。如果所有αE都是μ可測的,且αE與E的μ測度相等,則稱μ是左平移不變的。另一種理解基於測度的下述等價定義,即測度μ是K(G)(G上所有有緊支集的連續函式的全體)上的線性泛函,或稱K(G)上的積分,記為
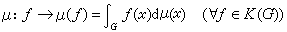 。 (3)
。 (3)
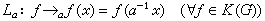 。
。
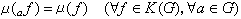 , (4)
, (4)
哈爾測度對怎樣的G是存在且惟一的,這是一個困惑人們多年的難題。早在19世紀末與20世紀初,許多數學家就對一些具體的群探討過這個問題。直到1933年,哈爾才在這個問題上邁出決定性的一步。他對任意有可列開基的局部緊群確立了哈爾測度的存在性。韋伊隨後用式(3)理解測度,從而對哈爾的結果作了整理與推廣,他對任意局部緊群確立了哈爾測度的存在性與(除一個常數倍數以外的)惟一性。此外,角谷靜夫與H.嘉當也在這個問題上作出過很重要的貢獻。
在交換群情形,左、右哈爾測度是一樣的,但在非交換情形卻不一樣了,它們由哈爾模函式相互聯繫。任取一個左哈爾測度dx,則對任意
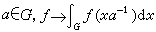 仍是K(G)上的一個左不變積分,故由惟一性知存在正數Δ(α),使
仍是K(G)上的一個左不變積分,故由惟一性知存在正數Δ(α),使 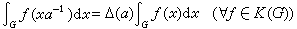 。 (5)
。 (5)
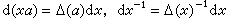 。
。
當考慮G 模某個子群(或正規子群)H 所得的齊性空間(或商群)G/H 時,其上的擬不變(或不變)測度可通過韋伊公式互相聯繫,因此群上調和分析可服務於齊性空間上的調和分析。
對偶群、對偶對象 它是拓撲群的某種意義下的對偶,可以用來研究拓撲群的結構,也可以用來定義傅立葉變換。
設G是交換的局部緊T2群,G到群T內的連續同態稱為一個(連續)特徵。譬如群R與T的所有(連續)特徵分別為
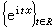 與
與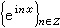 。設弿是G 的所有(連續)特徵的集合,可以定義 弿中的乘法為
。設弿是G 的所有(連續)特徵的集合,可以定義 弿中的乘法為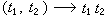 ,其中
,其中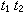
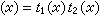 ,右邊是複數的普通乘法。還可以定義它的拓撲如下,對於所有ε>0與緊集K,令
,右邊是複數的普通乘法。還可以定義它的拓撲如下,對於所有ε>0與緊集K,令 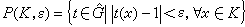
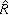 ,
,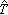 分別與R及Z拓撲同構。
分別與R及Z拓撲同構。 對非交換的局部緊T2群G,定義弿是G的所有連續不可約酉表示的等價類的全體,它在適當的拓撲下便稱為G的對偶對象。如G是緊群,則G的每個連續不可約酉表示U都是有限維的,即存在希爾伯特空間HU,dU=dimHU<∞,使得U(x)對每個x∈G都是HU上的酉運算元。此時弿的合適拓撲是離散拓撲。
關於這個對偶概念,有一個重要的事實是對偶定理。對交換群的龐特里亞金-范坎珀定理說,在如下的自然嵌入映射α下,
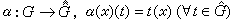 ,
,
群代數、測度代數、傅立葉代數、傅立葉-斯蒂爾傑斯代數 這些是群上調和分析最主要的研究對象。考慮一般局部緊 T2群G。L1(G)是G上(左)哈爾可積函式的等價類的全體,在普通線性運算,範數
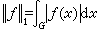 ,卷積乘法*
,卷積乘法* 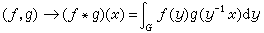 ,
,
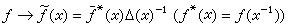
M(G)是G上所有復值正規有界波萊爾測度的全體在普通線性運算、全變差範數
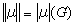 、卷積乘法*
、卷積乘法* 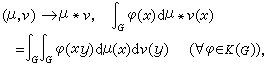
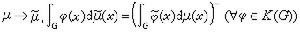 ,
,
傅立葉代數A(G)與傅立葉-斯蒂爾傑斯代數B(G)在交換群時不是新概念。它們是
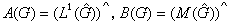 ,
,
傅立葉變換、傅立葉-斯蒂爾傑斯變換 設G是交換群,弿是它的對偶群,定義
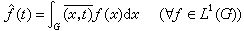 , (6)
, (6)
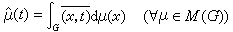 , (6)┡
, (6)┡
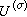 是任取的屬於σ的一個表示,記
是任取的屬於σ的一個表示,記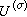 的表示空間為Hσ,其維數為dσ,
的表示空間為Hσ,其維數為dσ,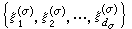 是任取的一組標準正交基,〈·,·〉表內積,記D是Hσ內如下定義的共軛線性運算元:
是任取的一組標準正交基,〈·,·〉表內積,記D是Hσ內如下定義的共軛線性運算元: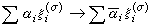 ,則
,則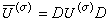 稱為
稱為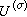 的共軛表示。則可以定義傅立葉變換為
的共軛表示。則可以定義傅立葉變換為 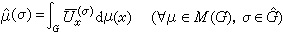 。 (7)
。 (7)
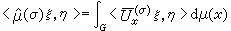 。
。
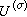 與D 的選取),但傅立葉變換的本質性質並不因此受影響。
與D 的選取),但傅立葉變換的本質性質並不因此受影響。 傅立葉變換有如下最基本事實(僅以交換群為例)。①μ→▇是M(G)到B(弿)上的,以及ƒ→弮是L1(G)到A(弿)上的巴拿赫對合代數同構,並且B(弿)中的元素都是一致連續的函式,A(弿)中的元素是無窮遠處趨於0的連續函式。後者稱為黎曼-勒貝格引理。此外“同構”蘊涵變換是一一的,即▇呏0推出μ呏0。這是傅立葉變換的惟一性定理。②對每個t∈弿,μ→▇(t)與ƒ→弮(t)分別是代數M(G)與L1(G)的復同態,特別有
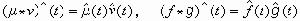 。
。
也有用交換巴拿赫代數的蓋爾范德理論來定義交換群上的傅立葉變換的。即ƒ∈L1(G)的傅立葉變換定義為ƒ作為巴拿赫代數L1(G)的元素的蓋爾范德變換。這種定義與前述定義是一致的。
普朗歇爾定理、 豪斯多夫-楊定理 普朗歇爾定理是交換群上調和分析中最重要而基本的定理,它說傅立葉變換F是L2(G)到L2(弿)上的一個等距同構運算元。其確切敘述為:G 與弿 上的哈爾測度可以規範化, 使得原在L1(G)∩L2(G) 上定義的傅立葉變換F 可以擴充為整個L2(G)到L2(弿)上的一個等距同構(仍記為F), 並且它的逆運算元正好是定義在L2(弿)上的傅立葉逆變換F-1:g→媝,
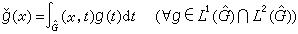 。
。
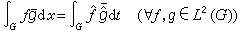 (8)
(8)
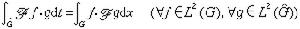 。 (8)┡
。 (8)┡
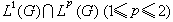 上的F可以連續地擴充為整個Lp(G)到L悜(弿)內的有界運算元,運算元範數不大於1,其中p┡是p的相伴數即滿足
上的F可以連續地擴充為整個Lp(G)到L悜(弿)內的有界運算元,運算元範數不大於1,其中p┡是p的相伴數即滿足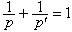 。
。 此時的帕舍伐爾關係為
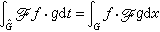 ,
, 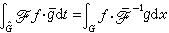 ,
, 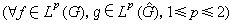
外爾-彼得定理 這是緊群上調和分析中最重要而基本的定理,它相當於對交換群的普朗歇爾定理。設G是緊群,dx是使G的測度為1的哈爾測度,σ∈弿,
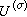 是屬於類σ中的一個不可約酉表示,Hσ是
是屬於類σ中的一個不可約酉表示,Hσ是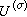 的表示空間,
的表示空間,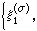
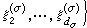 是Hσ中一組標準正交基,函式
是Hσ中一組標準正交基,函式 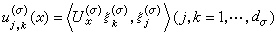 ,
,
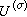 的表示函式。對於前面定義的
的表示函式。對於前面定義的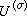 ,其表示函式即為
,其表示函式即為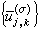 。
。 外爾-彼得定理 設G是緊群,則
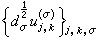 構成了L2(G)的一個完備標準正交系,此即,
構成了L2(G)的一個完備標準正交系,此即,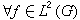 有
有 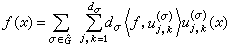 , (9)
, (9)
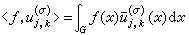 ;
;
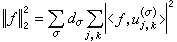 。 (10)
。 (10)
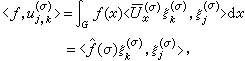
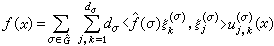 。 (9)┡
。 (9)┡
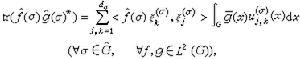 故有
故有 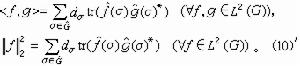
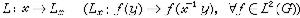 的不可約分解。用這種觀點看待古典調和分析雖然未免是小題大作,但對群上調和分析而言,這種觀點卻十分流行。以至有人認為調和分析就是用表示的分解來對函式空間進行分解的一種方法。以緊群為例來說明這種關係,符號沿用外爾-彼得定理中所述,記
的不可約分解。用這種觀點看待古典調和分析雖然未免是小題大作,但對群上調和分析而言,這種觀點卻十分流行。以至有人認為調和分析就是用表示的分解來對函式空間進行分解的一種方法。以緊群為例來說明這種關係,符號沿用外爾-彼得定理中所述,記 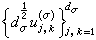 與
與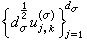
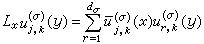
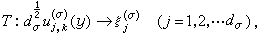
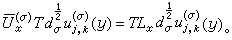
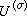 等價。故外爾-彼得定理的斷言
等價。故外爾-彼得定理的斷言 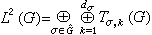 正與L的不可約分解
正與L的不可約分解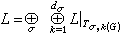 對應。
對應。 參考書目
E.Hewitt and K.R.Ross,Abstract harmonic Analysis,Vol.1~2,Springer-Verlag, Berlin, 1970.
Y.Katznelson,An Introduction to harmonic Analysis,Dover, New York, 1970.
W.Rudin,Fourier Analysis on Groups,Interscien-ce, New York, 1962.
G.Warner,harmonic Analysis on Semi-Simple Lie Groups,Vol, 1~2,Springer-Verlag, Berlin, 1972.
