概念
等價定義
設ƒ(x)是區間E上的函式。若對於任意屬於E的x,存在常數M>0,使得|ƒ(x)|≤M,則稱ƒ(X)是區間E上的有界函式。
例子
正弦函式sin x 和餘弦函式cos x為R上的有界函式,因為對於每個x∈R都有|sin x|≤1和|cos x|≤1
新的概念
下面介紹與有界函式概念相關的幾個概念。
相關概念
設函式f(x)是某一個實數集A上有定義,如果存在正數M 對於一切X∈A都有不等式|f(x)|≤M的則稱函式f(x)在A上有界,如果不存在這樣定義的正數M則稱函式f(x)在A上無界 設f為定義在D上的函式,若存在數M(L),使得對每一個x∈D有: ƒ(x)≤M(ƒ(x)≥L)
則稱ƒ在D上有上(下)界的函式,M(L)稱為ƒ在D上的一個上(下)界。
根據定義,ƒ在D上有上(下)界,則意味著值域ƒ(D)是一個有上(下)界的數集。又若M(L)為ƒ在D上的上(下)界,則任何大於(小於)M(L)的數也是ƒ在D上的上(下)界。根據確界原理,ƒ在定義域上有上(下)確界 。
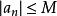 有界函式
有界函式一個特例是 有界數列,其中 X是所有自然數所組成的集合 N。所以,一個數列( a0, a1, a2, ... ) 是有界的,如果存在一個數 M> 0,使得對於所有的自然數 n,都有: 。
例子
由ƒ ( x)=sin x所定義的函式 f: R→ R是有界的。如果正弦函式是定義在所有複數的集合上,則不再是有界的。 函式 ( x不等於-1或1)是無界的。當 x越來越接近-1或1時,函式的值就變得越來越大。但是,如果把函式的定義域限制為[2, ∞).,則函式就是有界的。
函式是有界的。
任何一個連續函式 f:[0,1] → R都是有界的。 考慮這樣一個函式:當 x是有理數時,函式的值是0,而當 x是無理數時,函式的值是1。這個函式是有界的。有界函式並不一定是連續的。
性質
函式的有界性與其他函式性質之間的關係
函式的性質:有界性,單調性,周期性,連續性,可積性。
單調性
閉區間上的單調函式必有界。其逆命題不成立。
連續性
閉區間上的連續函式必有界。其逆命題不成立。
可積性
閉區間上的可積函式必有界。其逆命題不成立。
無界函式
類似的我們可以定義無界函式: 設ƒ為定義在D上的函式,若對於任何M(無論M多大),都存在x0∈D,使得|ƒ(x)|≥M。相關詳細定義請查看百度百科無界函式