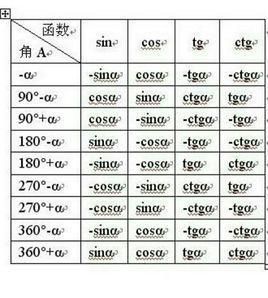
定義
常用的誘導公式有以下六組：
公式一
終邊相同的角的同一三角函式的值相等。
設α為任意銳角，弧度制下的角的表示：
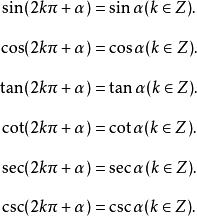誘導公式角度制下的角的表示：
sin (α+k·360°)=sinα（k∈Z）.
cos(α+k·360°)=cosα（k∈Z）.
tan (α+k·360°)=tanα（k∈Z）.
cot（α+k·360°）=cotα （k∈Z）.
sec（α+k·360°）=secα （k∈Z）.
csc（α+k·360°）=cscα （k∈Z）.
公式二
π+α的三角函式值與α的三角函式值之間的關係。
設α為任意角，弧度制下的角的表示：
sin（π+α）=－sinα.
cos（π+α）=－cosα.
tan（π+α）=tanα.
cot（π+α）=cotα.
sec（π+α）=－secα.
csc（π+α）=－cscα.
角度制下的角的表示：
sin（180°+α）=－sinα.
cos（180°+α）=－cosα.
tan（180°+α）=tanα.
cot（180°+α）=cotα.
sec（180°+α）=－secα.
csc（180°+α）=－cscα.
公式三
任意角α與 -α的三角函式值之間的關係：
sin（－α）=－sinα.
cos（－α）=cosα.
tan（－α）=－tanα.
cot（－α）=－cotα.
sec（－α）=secα.
csc (－α）=－cscα.
公式四
利用公式二和公式三可以得到π-α與α的三角函式值之間的關係：
弧度制下的角的表示：
sin（π－α）=sinα.
cos（π－α）=－cosα.
tan（π－α）=－tanα.
cot（π－α）=－cotα.
sec（π－α）=－secα.
csc（π－α）=cscα.
角度制下的角的表示：
sin（180°－α）=sinα.
cos（180°－α）=－cosα.
tan（180°－α）=－tanα.
cot（180°－α）=－cotα.
sec（180°－α）=－secα.
csc（180°－α）=cscα.
公式五
利用公式一和公式三可以得到2π-α與α的三角函式值之間的關係：
弧度制下的角的表示：
sin（2π－α）=－sinα.
cos（2π－α）=cosα.
tan（2π－α）=－tanα.
cot（2π－α）=－cotα.
sec（2π－α）=secα.
csc（2π－α）=－cscα.
角度制下的角的表示：
sin（360°－α）=－sinα.
cos（360°－α）=cosα.
tan（360°－α）=－tanα.
cot（360°－α）=－cotα.
sec（360°－α）=secα.
csc（360°－α）=－cscα.
公式六
π/2±α 及3π/2±α與α的三角函式值之間的關係：（⒈～⒋）
⒈ π/2+α與α的三角函式值之間的關係
弧度制下的角的表示：
sin（π/2+α）=cosα.
cos（π/2+α）=—sinα.
tan（π/2+α）=－cotα.
cot（π/2+α）=－tanα.
sec（π/2+α）=－cscα.
csc（π/2+α）=secα.
角度制下的角的表示：
sin（90°+α）=cosα.
cos（90°+α）=－sinα.
tan（90°+α）=－cotα.
cot（90°+α）=－tanα.
sec（90°+α）=－cscα.
csc（90°+α）=secα.
⒉ π/2－α與α的三角函式值之間的關係
弧度制下的角的表示：
sin（π/2－α）=cosα.
cos（π/2－α）=sinα.
tan（π/2－α）=cotα.
cot（π/2－α）=tanα.
sec（π/2－α）=cscα.
csc（π/2－α）=secα.
角度制下的角的表示：
sin (90°－α)=cosα.
cos (90°－α)=sinα.
tan (90°－α)=cotα.
cot (90°－α)=tanα.
sec (90°－α)=cscα.
csc (90°－α)=secα.
⒊ 3π/2+α與α的三角函式值之間的關係
弧度制下的角的表示：
sin（3π/2+α）=－cosα.
cos（3π/2+α）=sinα.
tan（3π/2+α）=－cotα.
cot（3π/2+α）=－tanα.
sec（3π/2+α）=cscα.
csc（3π/2+α）=－secα.
角度制下的角的表示：
sin（270°+α）=－cosα.
cos（270°+α）=sinα.
tan（270°+α）=－cotα.
cot（270°+α）=－tanα.
sec（270°+α）=cscα.
csc（270°+α）=－secα.
⒋ 3π/2－α與α的三角函式值之間的關係
弧度制下的角的表示：
sin（3π/2－α）=－cosα.
cos（3π/2－α）=－sinα.
tan（3π/2－α）=cotα.
cot（3π/2－α）=tanα.
sec（3π/2－α）=－cscα.
csc（3π/2－α）=－secα.
角度制下的角的表示：
sin（270°－α）=－cosα.
cos（270°－α）=－sinα.
tan（270°－α）=cotα.
cot（270°－α）=tanα.
sec（270°－α）=－cscα.
csc（270°－α）=－secα.
記憶
規律
公式一到公式五函式名未改變， 公式六函式名發生改變。
公式一到公式五可簡記為：函式名不變，符號看象限。即α+k·360°（k∈Z），﹣α，180°±α，360°－α的三角函式值，等於α的同名三角函式值，前面加上一個把α看成銳角時原函式值的符號。
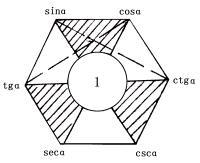三角公式的記憶圖上面這些誘導公式可以概括為：對於kπ/2±α(k∈Z)的三角函式值，
①當k是偶數時，得到α的同名函式值，即函式名不改變；
②當k是奇數時，得到α相應的余函式值，即sin→cos;cos→sin;tan→cot,cot→tan。（奇變偶不變）然後在前面加上把α看成銳角時原函式值的符號。（符號看象限）
例如：
sin(2π－α)=sin(4·π/2－α)，k=4為偶數，所以取sinα。
當α是銳角時，2π－α∈(270°，360°)，sin(2π－α)<0，符號為“－”。
所以sin(2π－α)=－sinα
口訣
奇變偶不變，符號看 象限 。
註：奇變偶不變（對k而言，指k取奇數或偶數），符號看象限（看原函式，同時可把α看成是銳角）。
公式右邊的符號為把α視為銳角時，角k·360°+α（k∈Z），-α、180°±α，360°-α所在象限的原三角函式值的符號可記憶：水平誘導名不變；符號看象限。
各種三角函式在四個象限的符號如何判斷，也可以記住口訣“一全正；二正弦(餘割)；三兩切；四餘弦(正割)”．
這十二字口訣的意思就是說：
第一象限內任何一個角的三角函式值都是“+”；
第二象限內只有正弦和餘割是“+”，其餘全部是“－”；
第三象限內只有正切和餘切是“+”，其餘函式是“－”；
第四象限內只有正割和餘弦是“+”，其餘全部是“－”。
一全正，二正弦，三雙切，四餘弦
