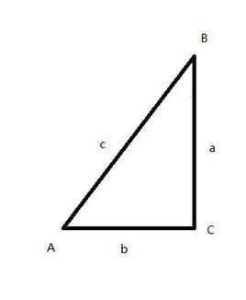
銳角三角函式定義
銳角角A的正弦（sin）,餘弦（cos）和正切（tan）,餘切（cot）以及正割（sec），餘割（csc）都叫做角A的銳角三角函式。
正弦（sin）等於對邊比斜邊；sinA=a/c
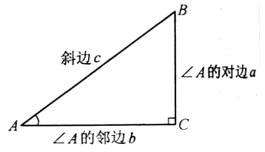銳角三角函式餘弦（cos）等於鄰邊比斜邊；cosA=b/c
正切（tan）等於對邊比鄰邊；tanA=a/b
餘切（cot）等於鄰邊比對邊；cotA=b/a
正割（sec)等於斜邊比鄰邊；secA=c/b
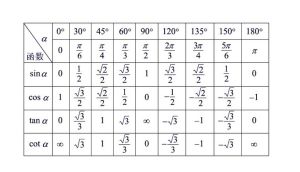特殊角的三角函式值表餘割(csc)等於斜邊比對邊。cscA=c/a
國中學習的 銳角三角函式值的定義方法是在直角三角形中定義的，所以在國中階段求銳角的三角函式值，都是通過構造直角三角形來完成的，即把這個角放到某個直角三角形中。到了高中三角函式值的求法是通過坐標定義法來完成的，這個時候角也擴充到了任意角。所謂銳角三角函式是指：我們國中研究的都是銳角 的 三角函式。國中研究的銳角 的 三角函式為：正弦（sin），餘弦（cos），正切（tan），餘切（cot）
函式值
特殊角
特殊角的三角函式值如下：
| 角度 | 0° | 30° | 45° | 60° | 90° |
| 正弦(sin) | 0 | 1/2 | √2/2 | √3/2 | 1 |
| 餘弦(cos) | 1 | √3/2 | √2/2 | 1/2 | 0 |
| 正切(tan) | 0 | √3/3 | 1 | √3 | 不存在 |
| 餘切(cot) | 不存在 | √3 | 1 | √3/3 | 0 |
| 正割(sec) | 1 | 2√3/3 | √2 | 2 | 不存在 |
| 餘割(csc) | 不存在 | 2 | √2 | 2√3/3 | 1 |
註：非特殊角的三角函式值，請查三角函式表。
取值範圍
θ是銳角：
0<1
0<1
tanθ>0
cotθ>0
變化情況
1.銳角三角函式值都是正值。
2.當角度在0°～90°間變化時，
正弦值隨著角度的增大（或減小）而增大（或減小） ，餘弦值隨著角度的增大（或減小）而減小（或增大） ；
正切值隨著角度的增大（或減小）而增大（或減小） ，餘切值隨著角度的增大（或減小）而減小（或增大）；
正割值隨著角度的增大（或減小）而增大（或減小），餘割值隨著角度的增大（或減小）而減小（或增大）。
3.當角度在0°≤A≤90°間變化時，0≤sinA≤1, 1≥cosA≥0；當角度在0°0。
關係式
同角三角函式
李善蘭三角函式展開式
（此公式又稱“李善蘭三角函式展開式”
或”李氏三角恆等式“）
tanα·cotα=1
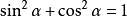銳角三角函式希臘三角函式公式
sinα/cosα=tanα=secα/cscα
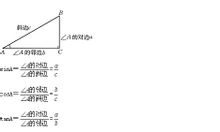直角三角形中的銳角三角形函式cosα/sinα=cotα=cscα/secα
1+(tanα)^2=(secα)^2
1+(cotα)^2=(cscα)^2
銳角三角函式誘導公式
sin（－α）=－sinα
cos（－α）=cosα
tan（－α）=－tanα
cot（－α）=－cotα
sin（π/2－α）=cosα
cos（π/2－α）=sinα
tan（π/2－α）=cotα
cot（π/2－α）=tanα
sin（π/2+α）=cosα
cos（π/2+α）=－sinα
tan（π/2+α）=－cotα
cot（π/2+α）=－tanα
sin（π－α）=sinα
cos（π－α）=－cosα
tan（π－α）=－tanα
cot（π－α）=－cotα
sin（π+α）=－sinα
cos（π+α）=－cosα
tan（π+α）=tanα
cot（π+α）=cotα
sin（3π/2－α）=－cosα
cos（3π/2－α）=－sinα
tan（3π/2－α）=cotα
cot（3π/2－α）=tanα
sin（3π/2+α）=－cosα
cos（3π/2+α）=sinα
tan（3π/2+α）=－cotα
cot（3π/2+α）=－tanα
sin（2π－α）=－sinα
cos（2π－α）=cosα
tan（2π－α）=－tanα
cot（2π－α）=－cotα
sin（2kπ+α）=sinα
cos（2kπ+α）=cosα
tan（2kπ+α）=tanα
cot（2kπ+α）=cotα(其中k∈Z)
二倍角、三倍角的正弦、餘弦和正切公式
Sin(2α)=2sinαcosα
Cos(2α)=（cosα）^2－(sinα)^2=2(cosα)^2－1=1－2(sinα)^2
Tan(2α)=2tanα/(1-tanα)
sin(3α)=3sinα-4sin^3α=4sinα·sin(60°+α)sin(60°-α)
cos(3α)=4cos^3α-3cosα=4cosα·cos(60°+α)cos(60°-α)
tan(3α)=(3tanα-tan^3α)/(1-3tan^2α)=tanαtan(π/3+α)tan(π/3-α)
公式
和差化積、積化和差公式有如下幾個：
sinα+sinβ=2sin[(α+β)/2]·cos[(α-β)/2]
sinα-sinβ=2cos[(α+β)/2]·sin[(α-β)/2]
cosα+cosβ=2cos[(α+β)/2]·cos[(α-β)/2]
cosα-cosβ=-2sin[(α+β)/2]·sin[(α-β)/2]
sinαcosβ=-[sin（α+β）+sin（α－β）]
sinαsinβ=-[cos（α+β）-cos（α-β）]/2
cosαcosβ=[cos（α+β）+cos（α-β）]/2
sinαcosβ=[sin（α+β）+sin（α-β）]/2
cosαsinβ=[sin（α+β）-sin（α-β）]/2
