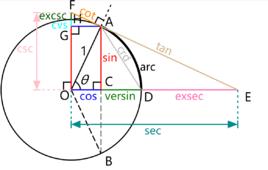
概述
如果三角形的一個角為90度,而另一個角的度數已知,那么第三個角的度數也就固定下來了,這是因為任何一個三角形三個角的度數之和總是180度。這樣,兩個銳角的度數之和為90度:它們互為餘角。這樣的三角形形狀已經完全確定下來,它們是一組度數相同的相似三角形。在度數確定的情況下,每個邊之間的比例也就隨之確定,無論三角形大小。如果其中一個邊的長度又為已知的話,那么其他兩條邊的長度也就確定。這些比例以角A的三角函式形式表示出來,其中a、b、c分別帶指三角形中對應三邊的長度:
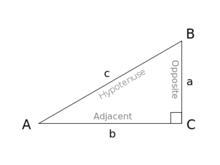 圖1.三角比
圖1.三角比(1)正弦函式(sin),定義為該角的對邊(opposite)與斜邊(hypotenuse)的比例。
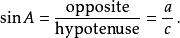 三角比
三角比(2)餘弦函式(cos),定義為該角的鄰邊(adjacent)與斜邊的比例。
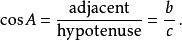 三角比
三角比(3)正切函式(tan),定義為該角的對邊與鄰邊的比例。
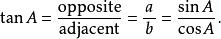 三角比
三角比其中,斜邊是指直角三角形中90度角所對的邊;它是該三角形中最長的邊,也是角A的一個鄰邊。對邊是角A所對的一條邊 。
這些函式的倒數分別被稱為 餘割(csc或cosec)、 正割(sec)和 餘切(cot):
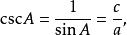 三角比
三角比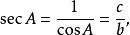 三角比
三角比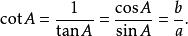 三角比
三角比它們的反三角函式分別為 arcsine、 arccosine和 arctangent。這些函式之間存在的數學關係被稱為三角恆等式。
通過使用這些函式,可以回答有關任意三角形的所有問題,只需使用正弦定理和餘弦定理。在已知兩條邊長以及它們夾角的度數,或是兩個角的度數以及一條邊長,或是知道三邊長度後,使用這些法則可以計算出其他角和邊。
相關定義及公式
銳角三角比的定義
sinA=角A的對邊/斜邊;
cosA=角A的鄰邊/斜邊;
tanA=角A的對邊/鄰邊;
cotA=角A的鄰邊/對邊。
同角的三角比關係
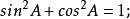 三角比
三角比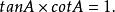 三角比
三角比互為餘角的三角比關係
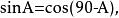 三角比
三角比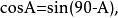 三角比
三角比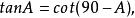 三角比
三角比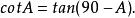 三角比
三角比直角三角形邊、角關係
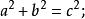 三角比
三角比邊與邊:
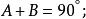 三角比
三角比角與角:
邊與角:銳角三角比概念;
所以,歷史上三角函式曾有三角比之稱,三角比不只是三角函式,兩者之間還有一定的差別。
誘導公式
公式一
設α為任意角,終邊相同的角的同一三角函式的值相等:
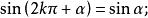 三角比
三角比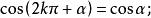 三角比
三角比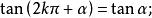 三角比
三角比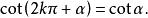 三角比
三角比公式二
 三角比
三角比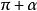 三角比
三角比 三角比
三角比設 為任意角, 的三角函式值與 的三角函式值之間的關係:
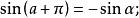 三角比
三角比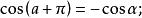 三角比
三角比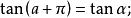 三角比
三角比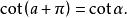 三角比
三角比公式三
 三角比
三角比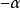 三角比
三角比任意角 與 的三角函式值之間的關係:
sin(-α)=-sinα
cos(-α)=cosα
tan(-α)=-tanα
cot(-α)=-cotα
公式四
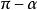 三角比
三角比 三角比
三角比利用公式二和公式三可以得到 與 的三角函式值之間的關係:
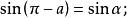 三角比
三角比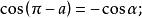 三角比
三角比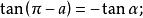 三角比
三角比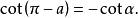 三角比
三角比公式五
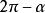 三角比
三角比 三角比
三角比利用公式一和公式三可以得到 與 的三角函式值之間的關係:
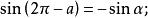 三角比
三角比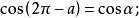 三角比
三角比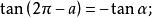 三角比
三角比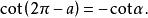 三角比
三角比誘導公式記憶口訣
上面這些誘導公式可以概括為:
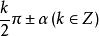 三角比
三角比對於 的個三角函式值,
 三角比
三角比 三角比
三角比①當 是雙數時,得到 的同名函式值,即函式名不改變;
 三角比
三角比 三角比
三角比②當 是單數時,得到 相應的余函式值,(單變雙不變)
然後在前面加上把α看成銳角時原函式值的符號(符號看象限) 。
其他三角函式知識
兩角和差公式
| 積化和差 | 和差化積 |
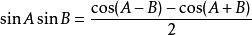 三角比 三角比 | 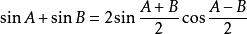 三角比 三角比 |
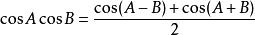 三角比 三角比 | 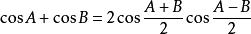 三角比 三角比 |
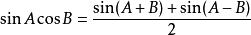 三角比 三角比 | 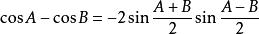 三角比 三角比 |
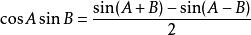 三角比 三角比 | 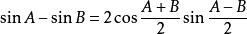 三角比 三角比 |
倍角公式
二倍角公式可以利用二角相等時的和角公式求得。
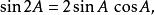 三角比
三角比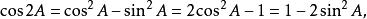 三角比
三角比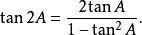 三角比
三角比利用和角公式也可以推導三倍角公式、四倍角公式等。
半角公式
半角公式可以利用餘弦函式的二倍角公式求得。
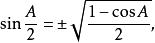 三角比
三角比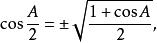 三角比
三角比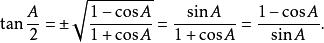 三角比
三角比積化和差公式
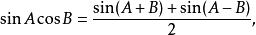 三角比
三角比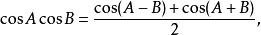 三角比
三角比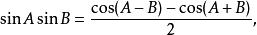 三角比
三角比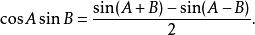 三角比
三角比和差化積公式
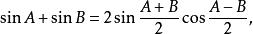 三角比
三角比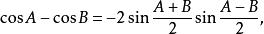 三角比
三角比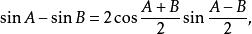 三角比
三角比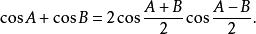 三角比
三角比