概念
第二變分公式(second variational formula)是刻畫能量泛函在臨界點附近屬性的重要公式。若f：M→N是調和映射，V∈Γ(f TN)是誘導向量叢f TN的一個具有緊緻支集的截面。f：M→N (-ε<t<ε)是單參數光滑映射族且滿足f=f和
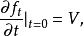第二變分公式則成立第二變分公式：
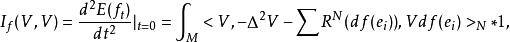第二變分公式式中{e}是M上么正標架場，R 是N上的黎曼曲率張量。若I(V，V)恆非負，則稱f為穩定調和映射。
能量泛函
能量泛函是映射的微分的模長平方的積分。設M和N為黎曼流形，f：M→N為光滑映射，f的能量定義為：
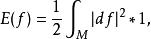第二變分公式式中df為f的微分，*1是M的體積元，E稱為能量泛函，
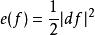第二變分公式稱為能量密度。
第一變分公式
第一變分公式是計算能量泛函的一階變分公式。若f：M→N是光滑映射，V∈Γ(f TN)是誘導向量叢f TN的一個截面，f：M→N (-ε<t<ε)是滿足f=f和
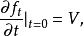第二變分公式的單參數光滑映射族，則當V具有緊緻支集時，成立第一變分公式：
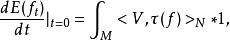第二變分公式式中τ(f)為f的張力場，〈 ， 〉表示N的黎曼內積，*1為M的體積元.這個公式表明τ(f)=0是能量泛函的歐拉-拉格朗日方程，而調和映射恰是能量泛函的臨界點。
調和映射
黎曼流形之間的一類十分重要的可微映射。設M和N為黎曼流形，f：M→N為光滑映射，若f的張力場τ(f)恆為零，則稱f為調和映射。由第一變分公式可知：調和映射是能量泛函的臨界點；反之，若f是能量泛函在每一個緊緻區域DM上關於保持邊界D不動的變分的臨界點，則f必是調和映射。另一方面，若將df看做M上取值於誘導叢fTN的1形式，這裡TN是N的切叢，則可以證明：當f為調和映射時，df為調和1形式；且當M為緊緻流形時，其逆亦真。因此，調和映射與非線性調和1形式理論有密切關係。調和映射有許多重要的特例，因而具有廣闊的背景。例如：
1.當N=R時，調和映射就是M上的調和函式。
2.當dim M=1時，調和映射就是N中的測地線。
3.當f為等距浸入時，f是調和映射的充分必要條件為f是極小浸入。
4.克勒流形間的全純映射必為調和映射。
5.具有雙不變黎曼度量的李群間的連續同態必為調和映射。
調和映射理論的基本問題是它的存在性問題，即，給定黎曼流形M和N間的一個映射f：M→N，在f的同倫類中是否存在調和映射φ?當M具有邊界M時，還要求在M上φ=f.調和映射的存在性依賴於M和N的拓撲和幾何性質以及f所在的同倫類。例如：
1.若M和N是緊緻黎曼流形且N的截曲率非正，則在M到N的任何映射同倫類中都存在一個調和映射，它的能量在該同倫類中為極小。
2.設M是二維環面，N是二維球面，若deg f=±1，則在f的同倫類中不存在調和映射。
調和映射方程τ(f)=0是一個半線性二階橢圓型方程組，對其整體解的存在性尚無一般理論可套用。因此，調和映射的存在性問題比較複雜，需要根據不同的情形採用不同的方法來解決。幾種主要的方法為：
1.利用熱方程的熱流法。
2.利用莫爾斯理論的攝動法。
3.利用正則性理論的變分學直接法。
4.化為常微分方程的方法。
5.利用全純映射的twistor方法。
與存在性問題相輔相成的是非常值調和映射的不存在性問題。這方面的結果與部分正則性定理相結合往往可以得到某種存在性定理。
作為幾何變分問題的解，調和映射的穩定性研究十分重要.若一個調和映射的第二變分恆非負，則稱為穩定調和映射.當n≥3時，從歐氏球面S到任何黎曼流形的穩定調和映射必是常值映射；另一方面，從任何緊緻黎曼流形到S(n≥3)的穩定調和映射也必是常值映射。對穩定調和映射的存在性與不存在性的研究，廣而言之，對調和映射的指標定理的研究是調和映射理論的一個重要方面。調和映射可用來刻畫黎曼流形的子流形的性質及構造。這種結果往往是通過對子流形的各種高斯映射的研究而得到。例如，R中子流形具有平行平均曲率的充分必要條件是它的高斯映射為調和映射.調和映射與全純映射的關係是調和映射理論的又一個重要方面，特別是複流形間的調和映射的全純性的研究已成為構造全純映射和解決很多重要數學問題的有力工具。反過來，通過twistor結構，利用全純映射來研究調和映射的構造和分類也已成為一種十分有效的方法。近40年來，調和映射理論得到了蓬勃的發展，它與復幾何、代數幾何、非線性分析和數學物理等領域互相滲透，正日益受到人們的重視，並發揮著重要的作用。
