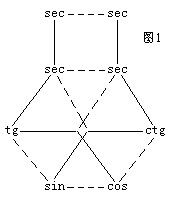
轉化公式
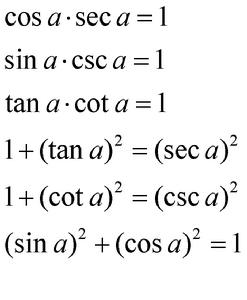 轉化公式
轉化公式sina*csca=1
tana*cota=1
1+(tana)^2=(seca)^2
1+(cota)^2=(csca)^2
(sina)^2+(cosa)^2=1
和角公式
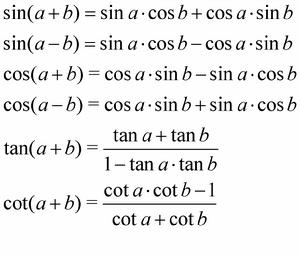 和角公式
和角公式sin(a-b)=sina*cosb-cosa*sinb
cos(a+b)=cosa*cosb-sina*sinb
cos(a-b)=cosa*cosb+sina*sinb
tan(a+b)=(tana+tanb)/(1-tana*tanb)
cot(a+b)=(cota*cotb-1)/(cota+cotb)
倍角公式
sin2a=2sina*cosa
cos2a=(cosa)^2-(sina)^2=2(cosa)^2-1=1-2(sina)^2
tan2a=2tana/[1-(tana)^2]
sin(3a)=3sina-4(sina)^3
cos(3a)=4(cosa)^3-3cosa
tan(3a)=[3tana-(tana)^3]/[1-3(tana^2)]
4.積化和差
sina*cosb=[sin(a+b)+sin(a-b)]/2cosa*sinb=[sin(a+b)-sin(a-b)]/2
cosa*cosb=[cos(a+b)+cos(a-b)]/2
sina*sinb=-[cos(a+b)-cos(a-b)]/2
和差化積
sina+sinb=2sin[(a+b)/2]cos[(a-b)/2]
sina-sinb=2sin[(a-b)/2]cos[(a+b)/2]
cosa+cosb=2cos[(a+b)/2]cos[(a-b)/2]
cosa-cosb=-2sin[(a+b)/2]sin[(a-b)/2]
萬能公式
令tan(a/2)=t
sina=2t/(1+t^2)
cosa=(1-t^2)/(1+t^2)
tana=2t/(1-t^2)
輔助角公式
Asint+bcost=(a^2+b^2)^(1/2)sin(t+r)
cosr=a/[(a^2+b^2)^(1/2)]
sinr=b/[(a^2+b^2)^(1/2)]
tanr=b/a
半角公式
sin^2(a/2)=(1-cos(a))/2
cos^2(a/2)=(1+cos(a))/2
tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))
誘導公式
sin(-α) = -sinα
cos(-α) = cosα
tan (—a)=-tanα
sin(π/2-α) = cosα
cos(π/2-α) = sinα
sin(π/2+α) = cosα
cos(π/2+α) = -sinα
sin(π-α) = sinα
cos(π-α) = -cosα
sin(π+α) = -sinα
cos(π+α) = -cosα
tanA= sinA/cosA
tan(π/2+α)=-cotα
tan(π/2-α)=cotα
tan(π-α)=-tanα
tan(π+α)=tanα
誘導公式記背訣竅:奇變偶不變,符號看象限