相量法

相量法是分析正弦穩態電路的一種方法。

概述

分析正弦穩態電路的一種方法。

1893年由德國人C.P.施泰因梅茨首先提出。此法是用稱為相量的複數來代表正弦量，將描述正弦穩態電路的微分（積分）方程變換成複數代數方程，從而在較大的程度上簡化了電路的分析和計算。

目前，在進行分析電路的正弦穩態時，人們幾乎都採用這種方法。

相量法的基本概念

正弦量(例如電流)可以表示成

式中符號īm 表示取後面的複數和複函數的虛部。
上式中的Imejψi是一個複數，用符號īm表示，稱為正弦量的振幅相量，其值為

īm=Imejψi=Imcosψi+jImsinψi(2)

用有效值代替振幅Im，得到有效值相量夒,其值為

(3)

顯然，在角頻率ω已知的情況下，可以用振幅相量或有效值相量代表一個正弦量。
正弦量與它的相量是一一對應的。給定了正弦量的瞬時值表達式

可以用式中振幅（或有效值）和初相角組成相量。īm＝Imejψi或ī＝Iejψi給定了相量，則īm＝Imejψi或ī＝Iejψi可以利用相量的模和幅角，以及已知的角頻率組成正弦量的瞬時值表達式

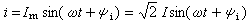
i=Imsin(ωt+ψi)=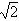Isin(ωt+ψi)

相量圖

相量是個複數，它在複平面上的圖形稱為相量圖。

複數在複平面上可以用一個矢量來表示，所以一個相量可以用複平面上的一個矢量來表示,如圖1所示。這種表示相量的圖稱為相量圖。若相量乘上ejwt,則表示該相量的矢量以角速度ω繞原點反時針鏇轉，於是得到一個鏇轉矢量,如圖2所示。這個鏇轉矢量稱為鏇轉相量，它在任何時刻在虛軸上的投影即為正弦量在該時刻的瞬時值，如圖3所示。

相量法

相量法

相量法

引入相量後，兩個同頻正弦量的加、減運算可以轉化為兩個相應的相量的加、減運算，相量的加減運算既可通過複數運算進行，也可在相量圖上按矢量加、減法則進行。另外，常遇到的正弦量乘以任意實常數和正弦量對時間求導數的運算可分別轉化為正弦量的相量乘以該任意實常數和正弦量的相量乘以的jω 運算。

基爾霍夫定律的相量形式

在正弦穩態下，基爾霍夫定律中的電流和電壓都是正弦量。用相量代表正弦電流和電壓後,基爾霍夫電流定律(KCL)和基爾霍夫電壓定律(KVL)分別變成
　 ∑ùm=0　或　∑u=0
　 ∑īm=0　或　∑i=0

電路元件的電壓相量與電流相量的關係

利用相量可將電路元件在時域中的電壓電流關係轉換成電壓相量與電流相量的關係。正弦電路中幾種常用元件的電壓相量與電流相量的關係如表所示。將正弦交流電路中每個電路均用對應的相量電路模型代替，便得到一個與原電路相對應的相量電路模型，這種模型對正弦交流電路的計算很有用處。

相量法

複數阻抗與複數導納

正弦交流電路中一個不含獨立電源且與外電路無耦合的一連線埠網路，其連線埠上的電壓相量與電流相量的比值定義為該網路的入端複數阻抗，簡稱阻抗。它的倒數定義為該網路的入端複數導納，簡稱導納，分別用符號Z和Y表示。

複數阻抗的實部稱為等效電阻，虛部稱為電抗，模稱為阻抗模，幅角稱為阻抗角,它們分別用符號R、X、|Z|、φ表示。複數導納的實部稱為等效電導，虛部稱為電納，模稱為導納模，幅角稱為導納角，它們分別用符號G、B、|Y|、φ┡表示，於是

Z =R+jX=|Z|ejφ

Y =G+jB=|Y|ejφ'

顯然，阻抗模等於連線埠電壓振幅（有效值）與連線埠電流振幅（有效值）的比值，阻抗角等於連線埠電壓超前連線埠電流的角度；導納模等於連線埠電流振幅(有效值)與連線埠電壓振幅（有效值）的比值，導納角等於連線埠電流超前連線埠電壓的角度。
電阻元件、電感元件和電容元件都是最簡單的一連線埠網路,若以ZR、ZL和ZC表示三者的複數阻抗，則按定義分別是

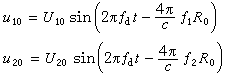
和

若以YR、YL和YC表示三者的複數導納,則按定義分別是

和

YC=jωC

顯然，複數阻抗（複數導納）的引入能使原非同類的元件歸併為都以複數阻抗（複數導納）來表征的同類元件，複數阻抗（複數導納）在交流電路中的地位與直流電路中的電阻（電導）相當。

相量法計算正弦交流電路

用此法計算電路有兩種方式，一種方式是，先象暫態分析那樣寫出電路的微分方程，再將方程中的正弦量和對正弦量的運算按規則改換成相量和對相量的運算，得出與原微分方程相對應的含相量的代數方程,然後,解此方程求出待求相量。另一種方式，也是通常所用的方式，則是在原電路的相量電路模型上,使用KCL和KVL的相量形式和電路元件電壓-電流關係的相量形式，如同計算直流電路那樣，直接列出含相量的代數方程，然後解此方程求出待求相量。兩種方式得到的解答完全一樣。有了相量便不難寫出原來需要求的正弦量。