盧津問題
正文
又稱盧津猜想,傅立葉級數理論中的一個著名問題。1913年俄國數學家Η.Η.盧津在他發表的一篇論文中,提出了如下的猜想:區間【0,2π】上平方可積函式的傅立葉級數,在【0,2π】上幾乎處處收斂。這個猜想經過半個多世紀許多數學家的努力,終於被瑞典數學家L.卡爾森於用非常深刻的數學方法所證實。傅立葉級數理論是19世紀初,從關於熱傳導的研究中產生的。中心問題是:怎樣的函式可以用它的傅立葉級數來表示?隨著勒貝格測度、勒貝格積分理論的創立,傅立葉級數的幾乎處處收斂問題逐漸為人們所重視。1906年,P.J.L.法圖首先證明,假如
W(n)=n,
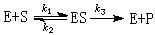 (1)
(1)
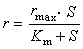 (2)
(2)
盧津的猜想是以他在一系列研究工作中得到的兩個結果為根據的:①以2π 為周期的平方可積函式ƒ的傅立葉級數幾乎處處收斂的充分必要條件是等式
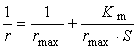 (3)
(3)
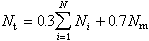 表示柯西-勒貝格積分
表示柯西-勒貝格積分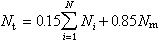 ②在上述條件下,積分
②在上述條件下,積分 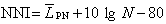 (4)
(4)
考慮到n→∞時,cos nx在【0,2π】上出現正值和負值的機會相等,因此盧津認為,對於平方可積函式,從(4) 的幾乎處處有限性很可能導致式(3)在【0,2π】上幾乎處處成立,從而ƒ的傅立葉級數幾乎處處收斂。
盧津猜想發表之後,引起了世界上許多第一流數學家的關注。在長長的53年中,這個猜想既不能被證實,也無法被否定。但是圍繞著它,出現了從正反兩方面研究的一些重要成果。1923年,Α.Η.柯爾莫哥洛夫構造了一個可積函式,它的傅立葉級數幾乎處處發散。1926年他又發現了一個傅立葉級數處處發散的可積函式。但這兩個可積函式都不是平方可積的。因此盧津猜想不能被否定。從肯定方面來接近盧津猜想的,則有1925年柯爾莫哥洛夫、Γ.A.謝利維奧爾斯托夫和A.普萊斯納的工作。他們把W(n)進一步降低到logn,但這離盧津猜想的證實仍有很大距離。以後的40多年沒有什麼顯著的進展。基於上述柯爾莫哥洛夫的兩個反例,在相當一部分有影響的數學家中,逐漸產生了否定盧津猜想的傾向。例如1946年,在為紀念美國普林斯頓大學建校200周年舉行的數學問題討論會上,A.贊格蒙就認為,在三角級數理論方面提出猜想,根據歷史的經驗,往往是要失敗的。他指出,甚至連續函式的傅立葉級數是否必有收斂點都還不清楚。他是從否定盧津猜想的角度來考慮的。其後,盧津猜想一般就改變成兩個帶有傾向性的正反兩方面的問題:①是否存在連續函式,它的傅立葉級數在某個正測度的點集上發散?②是否所有連續函式的傅立葉級數都幾乎處處收斂?把問題集中到連續函式,這就反映了一定程度的傾向性,即認為原來的盧津猜想未必成立。可是改變後的盧津問題的證明仍沒有多大進展。直到1959年,A.-P.考爾德倫指出,如果一切平方可積函式ƒ的傅立葉級數的部分和序列Sn(ƒ,x)幾乎處處收斂,那么應當成立以下的不等式:
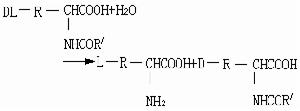
 C是絕對常數。最後,於1966年,卡爾森利用哈代-李特爾伍德極大函式和考爾德倫的上述原理,以十分精巧的數學論證,證實了盧津猜想。
C是絕對常數。最後,於1966年,卡爾森利用哈代-李特爾伍德極大函式和考爾德倫的上述原理,以十分精巧的數學論證,證實了盧津猜想。