極大函式

極大函式，又稱哈代-李特爾伍德極大函式。極大函式的研究對分析數學的發展起了很大作用，近年來又有許多推廣，並套用到數學的其他分支中去。

極大函式

正文

又稱哈代-李特爾伍德極大函式,由已知函式經一定運算（取平均）後取極大值所定義的函式，是由英國數學家G.H.哈代、J.E.李特爾伍德於20世紀30年代研究傅立葉級數時引進的。極大函式運算元M是指將函式ƒ 映為它的極大函式Mƒ的運算元。設ƒ(x)是Rn中的局部可積函式，那么稱下面的(Mƒ)(x)為ƒ的極大函式：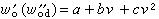

,

式中B(x,r)是以x為心、r為半徑的球，|B(x,r)|是球的體積,表示對r取上確界。可證明,極大函式(Mƒ)(x)是幾乎處處取有限值的，只要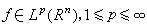；而且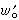,式中A是常數，僅與p，n有關。
從極大函式的定義可知,(Mƒ)(x)≥｜ƒ(x)｜幾乎處處成立。另一方面，只要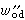,那么仍有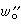。這說明， 極大函式(Mƒ)(x)雖比｜ƒ｜本身要大,但又“不太大”。正是這個重要性質,使得極大函式(Mƒ)(x)能有效地控制那些在lp上有界的運算元,最後可以通過函式本身的大小達到估計運算元的目的。
極大函式的研究對分析數學的發展起了很大作用，近年來又有許多推廣，並套用到數學的其他分支中去。

配圖

相關連線