定義
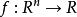 共軛函式
共軛函式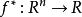 共軛函式
共軛函式設函式 ,定義函式 為
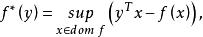 共軛函式
共軛函式 共軛函式
共軛函式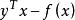 共軛函式
共軛函式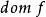 共軛函式
共軛函式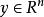 共軛函式
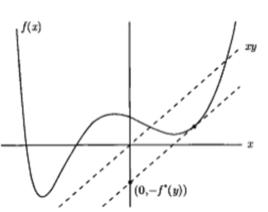
共軛函式此函式稱為函式 的 共軛函式。使上述上確界有限,即差值 在 有上界的所有 構成了共軛函式的定義域。圖1描述了此定義。
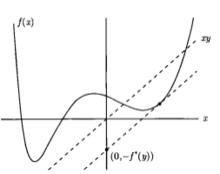 圖1
圖1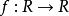 共軛函式
共軛函式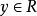 共軛函式
共軛函式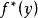 共軛函式
共軛函式 共軛函式
共軛函式 共軛函式
共軛函式 共軛函式
共軛函式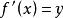 共軛函式
共軛函式 共軛函式
共軛函式圖1中,函式 以及某一 。共軛函式 是線性函式 和 之間的最大差值,見圖中虛線所示。如果 可微,在滿足 的點 處差值最大。
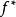 共軛函式
共軛函式 共軛函式
共軛函式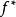 共軛函式
共軛函式 共軛函式
共軛函式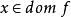 共軛函式
共軛函式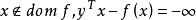 共軛函式
共軛函式顯而易見, 是凸函式,這是因為它是一系列 的凸函式(實質上是仿射函式)的逐點上確界。無論f是否是凸函式, 都是凸函式。(注意到這裡當 是凸函式時,下標 可以去掉,這是因為根據關於擴展值延伸的定義,對於 )。
基本性質
Fenchel不等式
 共軛函式
共軛函式 共軛函式
共軛函式從共軛函式的定義我們可以得到,對任意 和 ,如下不等式成立
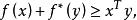 共軛函式
共軛函式 共軛函式
共軛函式上述不等式即為 Fenchel不等式(當 可微的時候亦稱為 Young不等式)。
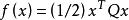 共軛函式
共軛函式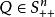 共軛函式
共軛函式以函式 為例,其中 ,我們可以得到如下不等式
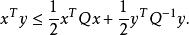 共軛函式
共軛函式共軛的共軛
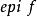 共軛函式
共軛函式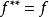 共軛函式
共軛函式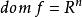 共軛函式
共軛函式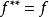 共軛函式
共軛函式上面的例子以及“共軛”的名稱都隱含了凸函式的共軛函式的共軛函式是原函式。也即:如果函式f是凸函式且f是閉的(即 是閉集),則 。例如,若 ,則我們有 ,即f的共軛函式的共軛函式還是f。
可微函式
可微函式f的共軛函式亦稱為函式f的 Legendre變換。(為了區分一般情況和可微情況下所定義的共軛,一般函式的共軛有時稱為 Fenchel共軛。)
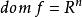 共軛函式
共軛函式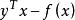 共軛函式
共軛函式 共軛函式
共軛函式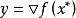 共軛函式
共軛函式 共軛函式
共軛函式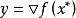 共軛函式
共軛函式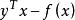 共軛函式
共軛函式 共軛函式
共軛函式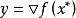 共軛函式
共軛函式設函式f是凸函式且可微,其定義域為 ,使 取最大的 滿足 ,反之,若 滿足 , 在 處取最大值。因此,如果 ,我們有
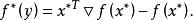 共軛函式
共軛函式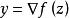 共軛函式
共軛函式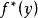 共軛函式
共軛函式所以,給定任意y,我們可以求解梯度方程 ,從而得到y處的共軛函式 。
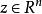 共軛函式
共軛函式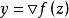 共軛函式
共軛函式我們亦可以換一個角度理解。任選 ,令 ,則
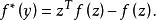 共軛函式
共軛函式伸縮變換和複合仿射變換
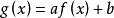 共軛函式
共軛函式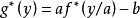 共軛函式
共軛函式若a>0以及b∈R, 的共軛函式為 。
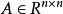 共軛函式
共軛函式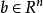 共軛函式
共軛函式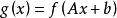 共軛函式
共軛函式設 非奇異, ,則函式 的共軛函式為
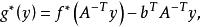 共軛函式
共軛函式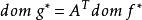 共軛函式
共軛函式其定義域為 。
獨立函式的和
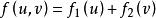 共軛函式
共軛函式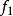 共軛函式
共軛函式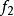 共軛函式
共軛函式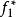 共軛函式
共軛函式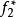 共軛函式
共軛函式如果函式 ,其中 和 是凸函式,且共軛函式分別為 和 ,則
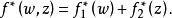 共軛函式
共軛函式換言之,獨立凸函式的和的共軛函式是各個凸函式的共軛函式的和。(“獨立”的含義是各個函式具有不同的變數。)
舉例分析
考慮R上一些凸函式的共軛函式。
仿射函式
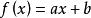 共軛函式
共軛函式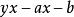 共軛函式
共軛函式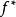 共軛函式
共軛函式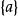 共軛函式
共軛函式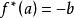 共軛函式
共軛函式,作為x的函式,若且唯若y=a,即為常數時 有界。因此,共軛函式 的定義域為單點集 ,且 。
負對數函式
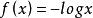 共軛函式
共軛函式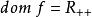 共軛函式
共軛函式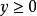 共軛函式
共軛函式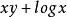 共軛函式
共軛函式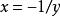 共軛函式
共軛函式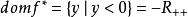 共軛函式
共軛函式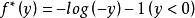 共軛函式
共軛函式,定義域為 。當 時,函式 無上界,當y<0時,在 處函式達到最大值。因此,定義域為 ,共軛函式為 。
指數函式
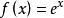 共軛函式
共軛函式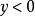 共軛函式
共軛函式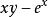 共軛函式
共軛函式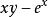 共軛函式
共軛函式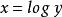 共軛函式
共軛函式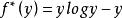 共軛函式
共軛函式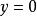 共軛函式
共軛函式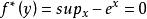 共軛函式
共軛函式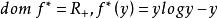 共軛函式
共軛函式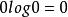 共軛函式
共軛函式,當 時,函式 無界。當y>0時,函式 在 處達到最大值。因此 。當 時, 。綜合起來, (我們規定 )。
負熵函式
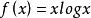 共軛函式
共軛函式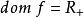 共軛函式
共軛函式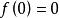 共軛函式
共軛函式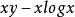 共軛函式
共軛函式 共軛函式
共軛函式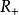 共軛函式
共軛函式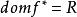 共軛函式
共軛函式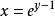 共軛函式
共軛函式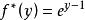 共軛函式
共軛函式,定義域為 (同上面討論, )。對所有 y,函式 關於 在 上有上界,因此 。在 處,函式達到最大值。因此 。
反函式
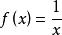 共軛函式
共軛函式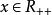 共軛函式
共軛函式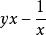 共軛函式
共軛函式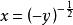 共軛函式
共軛函式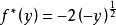 共軛函式
共軛函式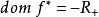 共軛函式
共軛函式, 。當y>0時, 無上界。當y=0時,函式有上確界0;當y<0時,在 處達到上確界。因此, 且 。