海水狀態方程
海水的現場密度略大於1。為了書寫方便起見,在海洋學中常用現場條件密度σSTp:=(-1)×103
在大氣壓p=0條件下的密度,稱為條件密度σT, 現場比容αSTp和現場密度成反比,即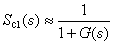
=(-0.9)×103
海水狀態方程在海洋學中通常用經驗公式來表達,有代表性的或在海洋學中廣泛使用的有:① 克努曾-埃克曼經典狀態方程式。1901年,M.H.C.克努曾提出了計算條件密度的海水狀態方程
σT=ΣT+(σ0+0.1324)【1-AT+BT(σ0-0.1324)】
1908年,V.W.埃克曼考慮了壓力的影響,提出計算現場 比容的關係式 上兩式中ΣT、AT、BT是與溫度有關的係數;σ0是與鹽度(或氯度)有關的係數;而μ決定於T、p和σ0。把這兩個式子綜合起來,就得到克努曾-埃克曼狀態方程,它曾廣泛套用在海洋學中。
② 皮耶克尼斯和桑德斯特勒姆狀態方程式。1910年,V.皮耶克尼斯和J.W.桑德斯特勒姆把現場比容看作是溫度、鹽度和壓力的函式,用泰勒級數展開後得到 式中諸δ表示改正值,已編成便於查算的數值表格。對比容也有類似的表達式。
③ UNESCO高壓海水狀態方程式。20世紀70年代,F.J.米勒羅等人按新鹽標計算實際鹽度S,並提出了新的狀態方程式 或者寫成 在一個標準大氣壓 (p=0)下的海水密度可由下列方程確定: 式中ρw為基準純水密度,K0和K分別為大氣壓下和壓力為p時的正割體積彈性模量,其中
K0=Kw+fS+gS3/2
A=Aw+iS+j0S3/2
B=Bw+mS
式中下角標W代表純水的量;Kw、Aw、Bw、ρw、b、c、f、g、i、m都是和溫度有關的係數;d0和jw為常數(見表)。此方程式的準確度相當高,能計算出某些熱力學參數,已被聯合國教科文組織的海洋學常用表和標準聯合專家小組第九次會議採納,並向全世界的各海洋學技術組織和學者推薦使用。它的適用範圍為:溫度-2~40°C,壓力 0~1000巴,鹽度0~42。 已提出的狀態方程式很多,但大都比較複雜,不便用在流體運動方程的熱力封閉系統中,因此一些學者提出不同的簡化的海水狀態方程式。例如О.И.馬馬耶夫在1964年發表的公式為σT=28.152-0.0735T-0.00469T2+(0.802-0.002T)(S-35)
它採用 A.德凡特在 1961年提出的壓力影響改正值σ′p=0.0046p,因此
σSTp=σT+σ′p
此式的使用範圍:溫度0~30°C,鹽度0~40,壓力0~1000巴。這種簡化式便於在建立海洋流體動力學的理論模式中使用。
參考書目
F.J.Millero,C.T.Chen,A.Bradshaw and K.Schlei-cher,A New High Pressure Equation of State forSeawater,Deepsea Research,Vol.27,No.3/4A,1980.