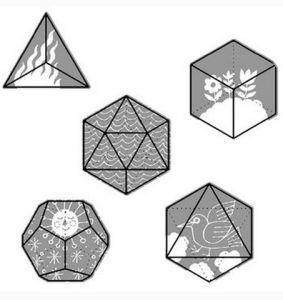
種類
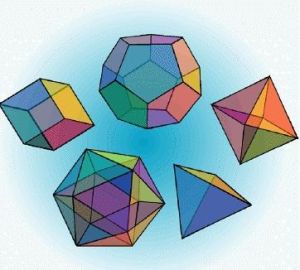 The Platonic Solids (柏拉圖立體/正多面體 )
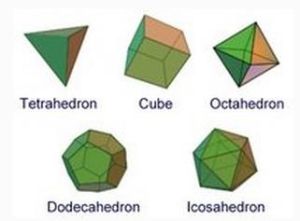
The Platonic Solids (柏拉圖立體/正多面體 )4個正三角形的正4面體;
6個正方形的正6面體(立方體);
8個正三角形的正8面體;
12個正五邊形的正12面體;
20個正三角形的正20面體。
發展史
 The Platonic Solids (柏拉圖立體/正多面體 )
The Platonic Solids (柏拉圖立體/正多面體 )不管怎么說,柏拉圖描繪了5種正多面體。他在《蒂邁歐篇》里講了如何拿正三角形,正方形和正五邊形來構造正多面體的面。柏拉圖的蒂邁歐(Timaeus),就是畢達格拉斯門下的洛克里的蒂邁歐。柏拉圖大概在訪問義大利時見過他。在柏拉圖的作品裡,蒂邁歐神秘地將4種易構造的多面體:正4面體,正6面體,正8面體,正20面體,配給恩培多克勒(Empedocles)的一切物質的四種基本“元素”:火氣水土。剩下的正20面體,就特意拿它來聯繫包圍我們的宇宙。
特性
1、內接於同一個球的正12面體的體積大於正20面體的體積,立方體的體積大於正八面體的體積。2、內接於同一個球的正12面體和正20面體具有這共同的內接球,立方體和正八面體也有共同的內接球。
3、如果正12面體,正20面體和立方體內接於同一個球,那么正12面體的體積與正20面體的體積之比,等於立方體邊長與正20面體的邊長之比。
4、如果正12面體與正20面體內接於同一個球,那么二者體積之比等於表面積之比。
5、內接於同一個球的正12面體和正20面體具有相等的表面周長。
證明
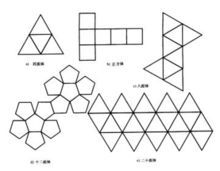 柏拉圖體展開圖
柏拉圖體展開圖設正多面體的每個面是正n邊形,每個頂點有m條棱。棱數E應是面數F與n的積的一半(每兩面共用一條棱),即
nF=2E--------------①
同時,E應是頂點數V與m的積的一半,即
mV=2E--------------②
由①、②,得
F=2E/n,V=2E/m,
代入歐拉公式V+F-E=2,
有2E/m+2E/n-E=2
整理後,得1/m+1/n=1/2+1/E.
由於E是正整數,所以1/E>0。因此
1/m+1/n>1/2--------------③
說明m,n不能同時大於3,否則③不成立。另一方面,由於m和n的意義(正多面體一個頂點處的棱數與多 邊形的邊數)知,m≥3且n≥3。因此m和n至少有一個等於3
當m=3時,因為1/n>1/2-1/3=1/6,n又是正整數,所以n只能是3,4,5
同理n=3,m也只能是3,4,5
所以有以下幾種情況:
由於上述5種多面體確實可以用幾何方法作出,而不可能有其他種類的正多面體,所以正多面體只有5種。