基本內容
正八面體是五種正多面體的第三種,有6個頂點和12條邊8個面。它由八個等邊三角形構成,也可以看做上、下兩個正方椎體黏合而成,每個正方椎體由四個三角形與一個正方形組成。正八面體正八面體展開圖正八面
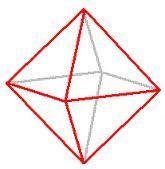 正八面體
正八面體體的對偶多面體是立方體。
正八面體內嵌在立方體中時,6個頂點分別位於立方體的面心:
正八面體體積 : 立方體體積=[(1/3)×高×底面積]×2 : 邊^3=(1/3)(n/2)(n^2/2)×2 : n^3=1 : 6
體積公式
若已知棱長a,則體積=(根號2/3)*a^3
面積公式
若已知棱長a,則表面積=(2根號3)*a^2
相關多面體
正八面體是正八面體家族的一員,與其對偶立方體隸屬同一家族:
| 對稱性 :[4,3], (*432) | [4,3], (432) | [1,4,3], (*332) | [4,3], (3*2) | | | | | | |
|---|---|---|---|---|---|---|---|---|---|
| | | | | | | | | | |
| | | | | | | | | | |
| {4,3} | t 0,1 {4,3} | t 1 {4,3} | t 1,2 {4,3} | {3,4} | t 0,2 {4,3} | t 0,1,2 {4,3} | s{4,3} | h{4,3} | h 1,2 {4,3} |
| 半正多面體的對偶 | | | | | | | | | |
| | | | | | | | | | |
| | | | | | | | | | |
| V4.4.4 | V3.8.8 | V3.4.3.4 | V4.6.6 | V3.3.3.3 | V3.4.4.4 | V4.6.8 | V3.3.3.3.4 | V3.3.3 | V3.3.3.3.3 |
正八面體還在拓撲上與其它三角形鑲嵌{3,n}相關聯:
| 多面體 | 歐式鑲嵌 | 雙曲鑲嵌 | | | | | | | |
|---|---|---|---|---|---|---|---|---|---|
| {3,2} | {3,3} | {3,4} | {3,5} | {3,6} | {3,7} | {3,8} | {3,9} | ... | {3,∞) |
作為截半正四面體[編輯]
正如以上所述,正八面體是截半正四面體,在這裡正八面體相鄰的面被塗上2種不同的顏色,在這種情況下,正八面體有正四面體對稱性A。
| 對稱性 :[3,3], (*332) | [3,3], (332) | | | | | | |
|---|---|---|---|---|---|---|---|
| | | | | | | | |
| | | | | | | | |
| {3,3} | t 0,1 {3,3} | t 1 {3,3} | t 1,2 {3,3} | t 2 {3,3} | t 0,2 {3,3} | t 0,1,2 {3,3} | s{3,3} |
| 半正多面體對偶 | | | | | | | |
| | | | | | | | |
| | | | | | | | |
| V3.3.3 | V3.6.6 | V3.3.3.3 | V3.6.6 | V3.3.3 | V3.4.3.4 | V4.6.6 | V3.3.3.3.3 |
注意到前五個正四面體的截頂體,它們可以被看作是四維超正方體長對角線垂直於平面時平面在不同高度截超正方體而得到的不同截面,如果設對角線長h=1時,這5種不同的截面分別出現於截面高度為(0,1/4]、3/8、1/2、5/8、[3/4,1)時,其中的正八面體截面是超正方體所有截面中體積最大的。
舉例
中心原子採取sp3d2等性雜化的微粒空間構型都屬於正八面體,例如SF6(六氟化硫)分子、IO6 5-(正高碘酸根)離子等。

