概念簡介
 示意圖
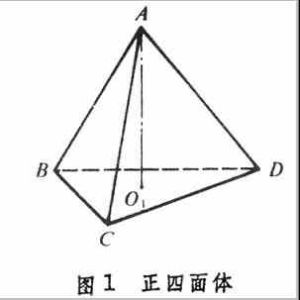
示意圖將立方體的其中四個頂點兩兩相連,而這四個頂點任何兩條都沒有落在立方體同一條的邊上,可得到一個正四面體,其邊長為立方體邊長的√2,其體積為立方體體積的1/3,從這裡看,正四面體是半立方體。正四面體是一個擁有無窮多個成員的多胞形家族—正單純形家族的3維成員。正四面體是一種稜錐體,即它可以被描述成由一個多邊形底面和連結底面和一個共同頂點的三角形面組成,對於正四面體來說,這個底面是正三角形,並且它的側面也都是正三角形,應此正四面體是正三稜錐。
正四面體是三維的正單純形(3-simplex),這意味著四面體是三維中最簡單的多面體,頂點數、棱數、面數比它少的多面體都只能成為退化多面體,同時在更高維的超空間中,任意4個頂點一定共在同一三維空間中,這4個頂點若不存在四點共面、三點共線和兩點重合的情況,一定能構成一個四面體,並且只要6條棱的長度確定了,四面體就被唯一確定了(即四面體具有穩定性。這是單純形面多胞形共有的一個基本特性),由此可知,一個四面體的6條棱長都相等,則其一定是一個正四面體。正四面體是柏拉圖立體中唯一一個所有頂點之間的距離都相等的,同時正四面體也是三維空間中使4個頂點每兩個頂點間距離相等的唯一方式。
定義
正四面體是由四個全等正三角形圍成的空間封閉圖形,所有棱長都相等。
它有4個面,6條棱,4個頂點。正四面體是最簡單的正多面體。
正三稜錐
正四面體屬於正三稜錐,但是正三稜錐只需要底面為正三角形,其他三個面是全等的等腰三角形就可以,不需要四個面全等且都是等邊三角形。
因此,正四面體又是特殊的正三稜錐。
基本性質
正四面體是一種柏拉圖多面體,正四面體與自身對偶。
正四面體的重心、四條高的交點、外接球、內切球球心共點,此點稱為中心。
正四面體有一個在其內部的內切球和七個與四個面都相切的旁切球,其中有三個旁切球球心在無窮遠處。
正四面體有四條三重鏇轉對稱軸,六個對稱面。
正四面體可與正八面體填滿空間,在一頂點周圍有八個正四面體和六個正八面體。
正四面體的對邊相互垂直。
化學中CH4,CCl4,SiH4等物質也是正四面體結構。
正四面體鍵角是109度28分,約為109.47°。
相關數據
當正四面體的棱長為a時,一些數據如下:
高:√6a/3。中心把高分為1:3兩部分。
表面積:√3a^2
體積:√2a^3/12
對棱中點的連線段的長:√2a/2
外接球半徑:√6a/4,正四面體體積占外接球體積的2*3^0.5/9*π,約12.2517532%。
內切球半徑:√6a/12,內切球體積占正四面體體積的π*3^0.5/18,約30.2299894%。
棱切球半徑:√2a/4.
兩條高夾角:2ArcSin(√6/3)=ArcCos(-1/3)=≈1.910633236249(弧度)或109°28′16″3942841664889。這一數值與三維空間中求最小面有關,也是蜂巢底菱形的鈍角的角度.
兩鄰面夾角:2ArcSin(√3/3)=ArcCos(1/3)≈1.23095(弧度)或70°31′43″60571,與兩條高夾角在數值上互補。
側棱與底面的夾角:ArcCos(√3/3)
正四面體的對棱相等。具有該性質的四面體符合以下條件:
1.四面體為對棱相等的四面體若且唯若四面體每對對棱的中點的連線垂直於這兩條棱。
2.四面體為對棱相等的四面體若且唯若四面體每對對棱中點的三條連線相互垂直。
3.四面體為對棱相等的四面體若且唯若四條中線相等。
建系方法
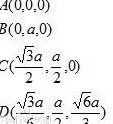 示意圖
示意圖以AB邊為y軸A為頂點ABC所屬平面為xOy面建系
四個頂點的坐標依次為