名詞簡介
正多面體的種數很少。多面體可以有無數，但正多面體只有正四面體、正六面體（正方體）、正八面體、正十二面體、正二十面體五種。其中面數最少的是正四面體，面數最多的是正二十面體。有些化學物質的結晶體呈正多面體的形狀，如食鹽的結晶體是正六面體，明礬的結晶體是正八面體。
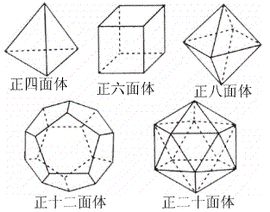正多面體古希臘的畢達哥拉斯學派曾對五種小多面體作過專門研究，並將研究成果拿給柏拉頓學校教授。故而，西方數學界也將這五種正多面
體稱為柏拉頓立體。
| 類型 | 面數 | 棱數 | 頂點數 | 每面邊數 | 每頂點棱數 |
| 正4面體 | 4 | 6 | 4 | 3 | 3 |
| 正6面體 | 6 | 12 | 8 | 4 | 3 |
| 正8面體 | 8 | 12 | 6 | 3 | 4 |
| 正12面體 | 12 | 30 | 20 | 5 | 3 |
| 正20面體 | 20 | 30 | 12 | 3 | 5 |
正多面體種類個數推導證明
代數幾何法
頂點數V，面數F，棱數E
設正多面體的每個面是正n邊形，每個頂點有m條棱。棱數E應是面數F與n的積的一半(每兩面共用一條棱)，即
nF=2E -------------- ①
正多面體同時，E應是頂點數V與m的積的一半，即
mV=2E -------------- ②
由①、②，得
F=2E/n, V=2E/m,
代入歐拉公式V+F-E=2，
有
2E/m+2E/n-E=2
整理後，得1/m+1/n=1/2+1/E.
由於E是正整數，所以1/E>0。因此
1/m+1/n>1/2 -------------- ③
正多面體說明m,n不能同時大於3，否則1/m+1/n<1/2，即
③不成立。另一方面，因為多邊形至少有三邊(n≥3)，而在每頂角處也至少有三邊(m≥3)。
但n>3，且r>3又是不可能的，因為那樣就要有
1/m+1/n<=1/4+1/4=1/2
故m和n中至少有一個等於3
當m=3時，因為1/n>1/2-1/3=1/6,n又是正整數，所以n只能是3，4，5
同理n=3，m也只能是3，4，5
所以有以下幾種情況:
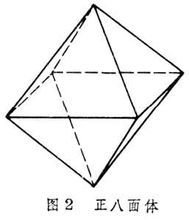
n=3，m=3 正四面體
正多面體n=4，m= 3 正六面體
n=3，m=4 正八面體
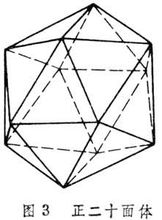
n=5，m=3 正十二面體
n=3，m=5 正二十面體
幾何法
由於上述5種多面體確實可以用幾何方法作出，而不可能有其他種類的正多面體
所以正多面體只有5種
正多面體相同表面積的四面體、六面體、正十二面體、以及正二十面體，其中體積最大的是:正二十面體。
或者這么證明:
假設每個頂點由m個正n邊形組成，由於每個頂點的角度必須小於360度，否則就成了平面了，可得:
m*(1-2/n)*180<360→m*(n-2)<2n→mn-2m-2n<0→mn-2m-2n+4<4→(m-2)(n-2)<4→m，n組合為:3，3;3，4;3，5;4，3;5，3幾種
名詞對偶性
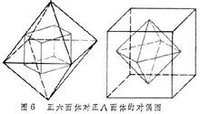
正多面體把一個正多面體每個面的中心連起來,可以得到一個新的多面體。這稱為正多面體的對偶性。如果原來是正六面體
,那么得到的是正八面體;如果原來是正八面體,那么得到的是正六面體.把這一性質稱為正六面體與正八面體對偶。正十二面體與正二十面體對偶。而正四面體則與自己對偶。
名詞公式
其中sqrt(x)表示x的算術平方根。
各多面體的體積如下：
V4=sqrt(2)/12*a^3
V6=a^3
V8=sqrt(2)/3*a^3
V12=(15+7sqrt(5))/4*a^3
V20=(15+5sqrt(5))/12*a^3
各多面體的表面積如下：
S4=sqrt(3)*a^2
S6=6*a^2
S8=2sqrt(3)*a^2
S12=（5sqrt(25+10sqrt(5))/4*a^2
S20=5sqrt(3)*a^2
