定義
有向直線，簡而言之，就是規定了正方向的直線。如數軸，直角坐標系中的x軸、y軸，都叫做有向直線。
任意一條直線，都可以規定兩個相反的方向，如果把其中的一個方向作為正方向，那么相反的方向就是負方向，像這樣規定了正方向的直線叫做 有向直線。
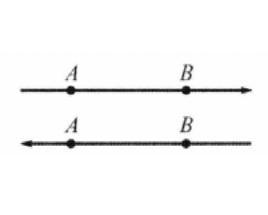
如果給直線定一個正向，則它叫做 有向直線。有向直線上的線段也“有向”，若A、B是直線上兩個不同的點，以A為始點以B為終點的矢量就是一個 有向線段，它的正向可以和直線正向相同或相反，但是如果不和直線相聯繫，空間一個非零矢不能叫做有向線段。
有向直線 有向直線
有向直線 有向直線 有向直線 有向直線 有向直線 有向直線 有向直線 有向直線 有向直線用矢量的話說，已給一條直線 和與 共線的非零矢 ，則若以 的方向為 的正向，則有向直線 與 同方向， 叫做有向直線的 定向矢，直線 上的矢量或有向線段，不是與 同向就是與 反向。
記法
有向直線
有向直線
有向直線 有向直線有向直線是規定了正方向的直線。直角坐標系中的 軸、 軸都是有向直線。表示有向直線，可順著直線的正向依次取兩點A、B，記為有向直線AB，也可以在箭頭的旁邊寫一個拉丁字母，記為有向直線。
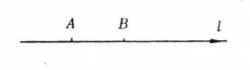圖1直線上矢量的代數長
有向直線
有向直線 有向直線 有向直線 有向直線 有向直線 有向直線 有向直線 有向直線 有向直線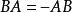
有向直線
有向直線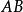
有向直線 有向直線有向直線上的矢量或有向線段不僅有長度還有表示方向的符號，當有向直線 上的非零矢 和 同向時， 的長度前加正號，即| |；當 的方向和 的相反時，加負號，即-| |，我們把 的帶符號的長度叫做 的 代數長。矢量 的代數長用 表示，顯然 ，我們也用記號 表示有向線段而不會引起混淆。
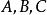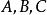有向直線 有向直線直線上的矢量相加，設 為同一直線上三個點，無論 怎樣排列，我們知道，總有關係
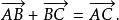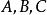有向直線 有向直線當我們作圖表示時，也可以看出：不論 有怎樣的相互位置，它們的 代數長也有類似的公式，
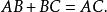有向直線我們還必須注意，空間中的矢量只有它在一條有向直線上才有所謂的代數長，零矢的代數長是零。
