基本介紹
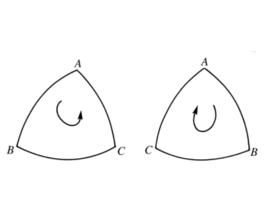
有向球面三角形亦稱定向球面三角形,是球面三角形的一種,指規定了三個頂點順序的球面三角形,有向球面三角形三個頂點的順序,規定了球面三角形三條邊的環行方向,這種環行方向有逆時針和順時針兩種(如圖1),通常取逆時針方向為正向,頂點順序為正向的有向球面三角形稱為 正向球面三角形或 正定向球面三角形;否則,稱為 負向球面三角形或 負定向球面三角形。兩個有向球面三角形在定向相同時稱為 同向球面三角形,定向相反時稱為反向球面三角形,有向球面三角形的三個內角自然而成為定向協合的有向角 。
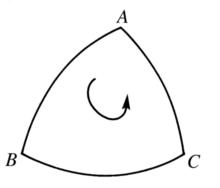 圖1(a)
圖1(a)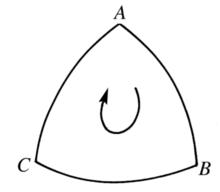 圖1(b)
圖1(b)相關概念
球面三角形
將球面上的三個點用大圓弧連線起來所圍成的圖形稱為 球面三角形,這三個點稱為 球面三角形的頂點,三個大圓弧稱為 球面三角形的邊, 球面三角形的角就是三個大圓弧兩兩相交而成的球面角。
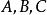 有向球面三角形
有向球面三角形由於連線兩點的大圓弧有兩個不同弧段,將球面上三個點用三段大圓弧連線起來圍成的圖形方式一般有8種,如表1所示陰影部分和無陰影部分。因此,在一般情況下,由三個點規定的球面三角形共有8個,其中一個球面三角形的三個邊都小於半個圓周,將這樣的球面三角形稱為 簡單球面三角 形,如圖(a)中的陰影部分所示,簡單球面三角形是經常用到的球面三角形 。
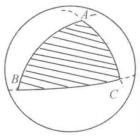 有向球面三角形 有向球面三角形 | 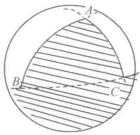 有向球面三角形 有向球面三角形 |
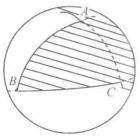 有向球面三角形 有向球面三角形 | 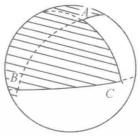 有向球面三角形 有向球面三角形 |
 有向球面三角形
有向球面三角形 有向球面三角形
有向球面三角形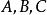 有向球面三角形
有向球面三角形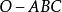 有向球面三角形
有向球面三角形如下圖所示,組成簡單球面三角形的三個大圓弧所在平面構成一個三面角,其頂點為球心,而其棱是由球心到球面三角形三個頂點的半徑。三面角的每一個平面角都可以用其相對的球面三角形的邊來度量,而兩個平面之間的夾角,即二面角等於其相應的球面三角形的球面角。
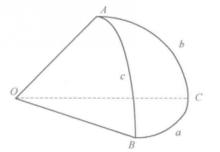 球面三角形
球面三角形有向球面角
有向球面角(oriented spherical angle)亦稱 定向球面角,球面幾何的基本概念之一,即規定了始邊和終邊的球面角,同一球面上的所有有向球面角可按下列方式分為兩類,構想觀察者站在有向球面角的頂點處(人在球外)觀察該有向球面角,這時必可發現下列兩種情況之一:
1.從始邊出發掃過角的內部旋轉到終邊的旋轉方向是逆時針的;
2.從始邊出發掃過角的內部旋轉到終邊的旋轉方向是順時針的。
通常規定逆時針方向是正方向,順時針方向是負方向,上述第一種有向球面角稱為 正向球面角,第二種有向球面角稱為 負向球面角.對兩個有向球面角,若它們的定向相同(即同為正向或同為負向),則稱它們是 同向球面角;否則,稱它們為 反向球面角‘’ .
有向角
有向角(directed angle)是三角學的基本概念之一。在平面幾何中,角被理解為從一點引出的兩條射線所組成的幾何圖形。如圖2,角α是從O點引出的兩條射線OA與OB組成的幾何圖形,角的概念是不斷擴充的,從運動的觀點出發,角被看做是一條射線在平面內繞其端點的旋轉量,並規定:射線的初始位置稱為角的始邊;射線的終止位置稱為角的終邊;射線的端點稱為角的頂點。引進上述概念後,就把角的始邊繞其頂點掃過角的內部到與終邊重合的旋轉方向稱為角的方向。因此,這種規定了方向的角就稱為 有向角,由於射線繞其端點的旋轉,如撥動時針,所以有兩個旋轉方向。對於有向角,通常規定:始邊按逆時針方向旋轉所成的角為正角;始邊按順時針方向旋轉所成的角為負角;始邊未作旋轉即與終邊重合的角為零角。
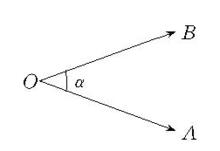 圖2
圖2球面角
球面角(spherical angle)是一種特殊的球面圖形,指由球面上一點和以此點為公共端點的兩條大圓弧所構成的球面圖形,公共端點稱為該球面角的頂點,兩條大圓弧稱為該球面角的邊。若球面角的頂點是A,它的兩條邊分別通過點B,C(如圖3),則該球面角可以記為∠BAC或∠CAB,球面角的度量有以下三種方法:
1.用由平面AOC和AOB所構成的二面角來度量。
2.用以球面角頂點為極的大圓,被該球面角截得的大圓弧BC之長來度量。
3.用過頂點的兩條邊的切線所夾的角(平面角)∠DAE來度量。
球面角也可以定義銳角、直角或鈍角,小於π/2的球面角稱為銳球面角,等於π/2的球面角稱為直球面角,大於π/2的球面角稱為鈍球面角 。
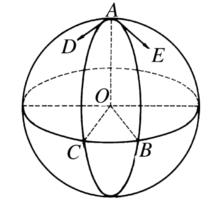 圖3
圖3有向球面二角形
球面二角形(spherical lune)亦稱月形或瓜瓣形,是一種特殊的球面圖形,球面上兩個對徑點和以這兩點為端點的兩個半大圓所圍成的球面圖形稱為球面二角形,構成球面二角形的兩個半大圓稱為它的邊,兩個對徑點稱為它的頂點,一個頂點和兩條邊所構成的球面角稱為它的角。
指規定了始邊和終邊的球面二角形叫有向球面二角形,對有向球面二角形兩頂點所在的直線指定一個正方向,構想一觀察者站在球面二角形的一個頂點處(其從腳到頭的方向和上述指定的正方向一致),觀察該球面二角形從始邊出發經球面二角形的內部到終邊的旋轉方向,這有兩種可能的情形:
1.旋轉方向是逆時針的;
2.旋轉方向是順時針的,
如果規定逆時針方向為正向,順時針方向為負向,則凡從始邊到終邊的旋轉方向是逆時針的球面二角形,稱為 正向球面二角形;否則,就稱其為 負向球面二角形 。