基本概念
復點、復直線 以複數為坐標的點或直線稱為復點或復直線。
復元素 復點和復直線統稱復元素。
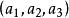 復直線
復直線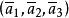 復直線
復直線共軛復元素 若 為一元素的齊次坐標時, 為另一同類元素的齊次坐標,則此二元素叫做共軛復元素。
兩個非無窮遠共軛復元素,其非齊次坐標必為共軛複數。
兩個共軛復元素的齊次坐標不一定為共軛複數,原因是齊次坐標可以相差一個常數因子 。
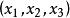 復直線
復直線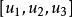 復直線
復直線復點 和復直線 的結合關係為
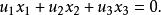 復直線
復直線相關概念
如果x,y這兩個數都是複數,那么就稱(x,y)為一個 有窮遠復點;如果x,y至少有一個是虛數,則稱(x,y)為一個 有窮遠虛點;如果x,y都是實數,則稱(x,y)為一個 有窮遠 實點。
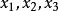 復直線
復直線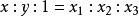 復直線
復直線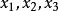 復直線
復直線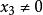 復直線
復直線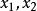 復直線
復直線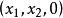 復直線
復直線可對有窮遠復點(x,y)定義齊次坐標為:如果複數 滿足 ,則稱( )為有窮遠復點(x,y)的齊次坐標.此時 。如果 為複數,則稱 為無窮遠復點的齊次坐標。有窮遠復點與無窮遠復點統稱為復點。所有復點的集合稱為復射影平面。復點的齊次坐標不是唯一;同一復點的齊次坐標可以相差一個非零復因子;(0,0,0)不是任何復點的齊次坐標。
下面我們用i表示虛數單位。
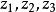 復直線
復直線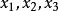 復直線
復直線一個虛齊次坐標有可能代表一個實點。例如(i,2i,-i)就代表實點(-1,-2)。一個復齊次坐標( 鉑)代表實點的充分必要條件是它與實齊次坐標( )成比例。
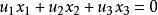 復直線
復直線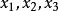 復直線
復直線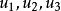 復直線
復直線滿足齊次方程 的復點( )的集合稱為 復直線,其係數[ ]稱為該復直線的齊次坐標。
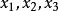 復直線
復直線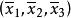 復直線
復直線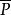 復直線
復直線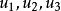 復直線
復直線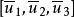 復直線
復直線設復點P的齊次坐標為( ),則稱齊次坐標為的點為點P的共軛復點;設復直線l的齊次坐標為[],則稱齊次坐標為]的復直線l為復直線l的共軛復直線。
我們把點I(1,i,0)和點J(1,-i,0)叫做 圓點,過圓點I或J的直線叫做 迷向直線。
共軛復點和共軛復直線統稱為 共軛復元素。注意,一對同類共軛復元素的齊次坐標不
必為共軛複數,因為同一點的齊次坐標可以相差一個非零複數。例如(2,i,1-i)與(2+2i,1-i,2i)是一對共軛復點的齊次坐標,這是因為
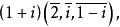 復直線
復直線(2+2i,1-i,2i)=(1+i)(2,-i,1+i)=.
但顯然(2,i,1-i)與(2+2i,1-i,2i)不是共軛複數 。
相關定理
定理1 一元素為實元素的充要條件是該元素與其共軛復元素重合。
 復直線
復直線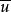 復直線
復直線定理2 如果一點x在一直線u上,則共軛復點必在共軛直線上。
定理3 兩共軛復直線的交點為一實點,兩共軛復點的連線為一實直線。
推論 在一復直線上有唯一一個實點,過一復點有唯一一條實直線 。
註:一實直線上的點或為實點或為一共軛復點;過一實點的直線或為一實直線或為一共軛復直線。

