定義
基本定義
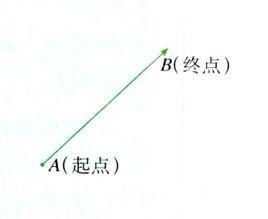
定義1 當一條線段的一個端點被指定為起點.而另一個端點被指定為終點,並且規定由起點到終點的方向叫作這條線段的方向時,那么,這種線段叫作有向線段 .
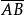 有向線段
有向線段也可以簡單地說,規定了起點和終點的線段叫作有向線段.或者說,規定了方向的線段叫作有向線段.起點為A,終點為B的有向線段用符號 表示.
起點與終點重合的有向線段叫作零有向線段.零有向線段的方向可以任意指定.
定義2 如果兩條有向線段方向相同.並且長度相等,就說這兩條有向線段相等;規定零有向線段都是相等的 .
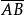 有向線段
有向線段 有向線段
有向線段必須注意, 與 是不相等的.因為它們的方向相反.
配置在軸上的有向線段
定義3 當一條直線的正向被指定了以後,那么.這種直線叫作軸(有向直線) .
若配置在軸上的有向線段的方向和軸的正向相同,那么,這種位置的有向線段叫作軸上的正方向的有向線段;若有向線段的方向和軸的正向相反,那么,這種位置的有向線段叫作軸上的負方向的有向線段.
定義4 軸上的正方向的有向線段的長度,負方向的有向線段的長度的相反數,叫作這條有向線段的數值(代數長).規定零有向線段的數值為0 .
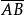 有向線段
有向線段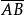 有向線段
有向線段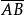 有向線段
有向線段有向線段 的數值用符號“值 ”或“AB”表示,而長度(或叫作模)用符號“∣ ∣”表示。
相關定理
定理1 設A,B是軸上的任意兩點,則AB=﹣BA
即:AB+BA=0
定理2 (沙爾(Mishel Schasles)定理) 設A,B,C是軸上的任意三點,則以下的關係式總成立,即
AB+BC=AC
證明 分以下幾種情形證明.
(1)B在A,C之間,並且由A到B的方向和軸的正向相同(圖(a)).
由初等幾何知道:∣AB∣+∣BC∣=∣AC∣(∣ AB∣表示線段AB的長度),
而
 有向線段
有向線段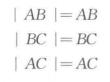 有向線段
有向線段所以有:AB+BC=AC
(2)B在A,C之間,並且由A到B的方向和軸的正向相反(圖(b)).由(1)知道:CB+BA=CA,而由定理1知
 有向線段
有向線段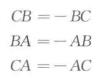 有向線段
有向線段所以有:AB+BC=AC
其餘各種情形的證明,可按下圖自己完成.
 有向線段
有向線段 有向線段
有向線段 有向線段
有向線段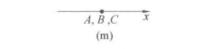 有向線段
有向線段 有向線段
有向線段 有向線段
有向線段 有向線段
有向線段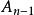 有向線段
有向線段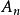 有向線段
有向線段推論(沙爾定理的推廣) 設,,,......,,(n≥3)是軸上的任意n個點.則關係式
 有向線段
有向線段總成立.
有向線段三要素
起點、方向和長度,知道了有向線段的起點,它的終點就被方向和長度唯一確定 。
有向線段與向量
有向線段不等同於向量。二者的區別是:向量可用有向線段來表示,每一條有向線段對應著一個向量,但每一個向量對應著無數多條有向線段 。