簡介
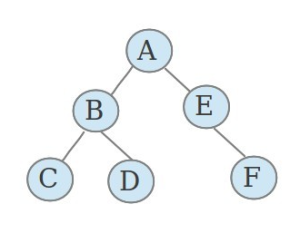 二叉樹
二叉樹辨析
二叉樹是樹的一種特殊情形?,儘管其與樹有許多相似之處,但樹和二叉樹有兩個主要差別:
1.樹中結點的最大度數沒有限制,而二叉樹結點的最大度數為2;
2.樹的結點無左、右之分,而二叉樹的結點有左、右之分。
樹
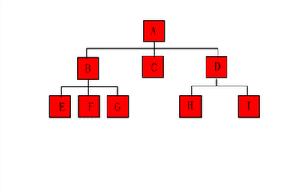
樹是一種重要的非線性數據結構,直觀地看,它是數據元素(在樹中稱為結點)按分支關係組織起來的結構,很象自然界中的樹那樣。樹結構在客觀世界中廣泛存在,如人類社會的族譜和各種社會組織機構都可用樹形象表示。樹在計算機領域中也得到廣泛套用,如在編譯源程式時,可用樹表示源程式的語法結構。又如在資料庫系統中,樹型結構也是信息的重要組織形式之一。一切具有層次關係的問題都可用樹來描述。
樹結構的特點是:它的每一個結點都可以有不止一個直接後繼,除根結點外的所有結點都有且只有一個直接前驅。以下具體地給出樹的定義及樹的數據結構表示。
樹的定義
樹是由一個或多個結點組成的有限集合,其中:
⒈必有一個特定的稱為根(ROOT)的結點;
⒉剩下的結點被分成n>=0個互不相交的集合T1、T2、......Tn,而且,這些集合的每一個又都是樹。樹T1、T2、......Tn被稱作根的子樹(Subtree)。
樹的遞歸定義如下:(1)至少有一個結點(稱為根)(2)其它是互不相交的子樹
1.樹的度——也即是寬度,簡單地說,就是結點的分支數。以組成該樹各結點中最大的度作為該樹的度,樹中度為零的結點稱為葉結點或終端結點。樹中度不為零的結點稱為分枝結點或非終端結點。除根結點外的分枝結點統稱為內部結點。
2.樹的深度——組成該樹各結點的最大層次,其深度為3;
3.森林——指若干棵互不相交的樹的集合,如上圖,去掉根結點A,其原來的二棵子樹T1、T2、T3的集合{T1,T2,T3}就為森林;
4.有序樹——指樹中同層結點從左到右有次序排列,它們之間的次序不能互換,這樣的樹稱為有序樹,否則稱為無序樹。
樹的表示
樹的表示方法有許多,常用的方法是用括弧:先將根結點放入一對圓括弧中,然後把它的子樹由左至右的順序放入括弧中,而對子樹也採用同樣的方法處理;同層子樹與它的根結點用圓括弧括起來,同層子樹之間用逗號隔開,最後用閉括弧括起來。如上圖可寫成如下形式:
(A(B(E(K,L),F),C(G),D(H(M),I,J)))
二叉樹
基本形態
二叉樹也是遞歸定義的,其結點有左右子樹之分,邏輯上二叉樹有五種基本形態:
(1)空二叉樹——(a);
(2)只有一個根結點的二叉樹——(b);
(3)只有左子樹——(c);
(4)只有右子樹——(d);
(5)完全二叉樹——(e)
注意:儘管二叉樹與樹有許多相似之處,但二叉樹不是樹的特殊情形。
重要概念
(1)完全二叉樹——若設二叉樹的高度為h,除第h層外,其它各層(1~h-1)的結點數都達到最大個數,第h層有葉子結點,並且葉子結點都是從左到右依次排布,這就是完全二叉樹。
(2)滿二叉樹——除了葉結點外每一個結點都有左右子葉且葉子結點都處在最底層的二叉樹。
(3)深度——二叉樹的層數,就是深度。
性質
(1)在二叉樹中,第i層的結點總數不超過2^(i-1);
(2)深度為h的二叉樹最多有2^h-1個結點(h>=1),最少有h個結點;
(3)對於任意一棵二叉樹,如果其葉結點數為N0,而度數為2的結點總數為N2,則N0=N2+1;
(4)具有n個結點的完全二叉樹的深度為int(log2n)+1
(5)有N個結點的完全二叉樹各結點如果用順序方式存儲,則結點之間有如下關係:
若I為結點編號則如果I>1,則其父結點的編號為I/2;
如果2*I<=N,則其左兒子(即左子樹的根結點)的編號為2*I;若2*I>N,則無左兒子;
如果2*I+1<=N,則其右兒子的結點編號為2*I+1;若2*I+1>N,則無右兒子。
(6)給定N個節點,能構成h(N)種不同的二叉樹。
h(N)為卡特蘭數的第N項。h(n)=C(n,2*n)/(n+1)。
(7)設有i個枝點,I為所有枝點的道路長度總和,J為葉的道路長度總和J=I+2i
存儲結構
(1)順序存儲方式
typenode=record
data:datatype
l,r:integer;
end;
vartr:array[1..n]ofnode;
(2)鍊表存儲方式,如:
typebtree=^node;
node=record
data:datatye;
lchild,rchild:btree;
end;
實現
範例二叉樹:
A
BC
DE
此樹的順序結構為:ABCD##E
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
intmain()
{
node*p=newnode;
node*p=head;
head=p;
stringstr;
cin>>str;
creat(p,str,0)//默認根節點在str下標0的位置
return0;
}
//p為樹的根節點(已開闢動態記憶體),str為二叉樹的順序存儲數組ABCD##E或其他順序存儲數組,r當前結點所在順序存儲數組位置
voidcreat(node*p,stringstr,intr)
{
p->data=str[r];
if(str[r*2+1]=="#"||r*2+1>str.size()-1)p->lch=NULL;
else
{
p->lch=newnode;
creat(p->lch,str,r*2+1);
}
if(str[r*2+2]=="#"||r*2+2>str.size()-1)p->rch=NULL;
else
{
p->rch=newnode;
creat(p->rch,str,r*2+2);
}
}
二叉樹
二叉樹很像一株倒懸著的樹,從樹根到大分枝、小分枝、直到葉子把數據聯繫起來,這種數據結構就叫做樹結構,簡稱樹。樹中每個分叉點稱為結點,起始結點稱為樹根,任意兩個結點間的連線關係稱為樹枝,結點下面不再有分枝稱為樹葉。結點的前趨結點稱為該結點的"雙親",結點的後趨結點稱為該結點的"子女"或"孩子",同一結點的"子女"之間互稱"兄弟"。
普通樹轉二叉樹,一般採用左“子女”右“兄弟”的方式來轉化。
轉化規則:
普通樹為有序樹T,將其轉化成二叉樹T’如下:
⑴T中的結點與T’中的結點一一對應,即T中每個結點的序號和值在T’中保持不變;
⑵T中某結點v的第一個兒子結點為v1,則在T’中v1為對應結點v的左兒子結點;
⑶T中結點v的兒子序列,在T’中被依次連結成一條開始於v1的右鏈;
由上述轉化規則可以看出,一棵有序樹轉化成二叉樹的根結點是沒有右子樹的,並且除保留每個結點的最左分支外,其餘分支應去掉,然後從最左的兒子開始沿右兒子方向依次連結該結點的全部兒子。
還有一種比較有趣的方法
1)在樹的所有兄弟結點上添加一條水平線
2)刪去所有除左子樹之外的所有父到子之間的樹枝或者說成刪去父結點到除最左陔子之外的所有其它孩子之間的樹枝。
3)將添加的水平線順時間轉動45度。
剛開始是
..0
/|\
000
增加上水平線
...0
./|\
0--0--0
刪除父到子除最左之外的所有樹枝
...0
./
0-0-0
再將連線轉動45度成為最終的二叉樹為
.......0
..../
..0
....\
......0
........\
..........0
即在任一個結點上除了左子樹外,左子樹的右邊的兄弟將全部連線成為左子樹的右子樹舉例如
二叉樹
..A
/|\
BCD
應上面我說的除左子樹外,左子樹的右兄弟都連線成他的子。成為A為根,B是他的左子不變,C成為B的右子樹D又連成C的右子樹,結果為
......A
..../
..B
....\
......C
........\
..........D
完成
註:“.”為空格。
完全二叉樹
對滿二叉樹,從第一層的結點(即根)開始,由下而上,由左及右,按順序結點編號,便得到滿二叉樹的一個順序表示。據此編號,完全二叉樹定義如下:一棵具有n個結點,深度為K的二叉樹,若且唯若所有結點對應於深度為K的滿二叉樹中編號由1至n的那些結點時,該二叉樹便是完全二叉樹。
二叉樹遍歷
遍歷是對樹的一種最基本的運算,所謂遍歷二叉樹,就是按一定的規則和順序走遍二叉樹的所有結點,使每一個結點都被訪問一次,而且只被訪問一次。由於二叉樹是非線性結構,因此,樹的遍歷實質上是將二叉樹的各個結點轉換成為一個線性序列來表示。
設L、D、R分別表示遍歷左子樹、訪問根結點和遍歷右子樹,則對一棵二叉樹的遍歷有三種情況:DLR(稱為先根次序遍歷),LDR(稱為中根次序遍歷),LRD(稱為後根次序遍歷)。
(1)先序遍歷
首先訪問根,再先序遍歷左(右)子樹,最後先序遍歷右(左)子樹,C語言代碼如下:
1
2
3
4
5
6
7
8
voidXXBL(tree*root)
{
//DoSomethingwithroot
if(root->lchild!=NULL)
XXBL(root->lchild);
if(root->rchild!=NULL)
XXBL(root->rchild);
}
(2)中序遍歷
首先中序遍歷左(右)子樹,再訪問根,最後中序遍歷右(左)子樹,C語言代碼如下
1
2
3
4
5
6
7
8
voidZXBL(tree*root)
{
if(root->lchild!=NULL)
ZXBL(root->lchild);
//DoSomethingwithroot
if(root->rchild!=NULL)
ZXBL(root->rchild);
}
(3)後序遍歷
首先後序遍歷左(右)子樹,再後序遍歷右(左)子樹,最後訪問根,C語言代碼如下
1
2
3
4
5
6
7
8
voidHXBL(tree*root)
{
if(root->lchild!=NULL)
HXBL(root->lchild);
if(root->rchild!=NULL)
HXBL(root->rchild);
//DoSomethingwithroot
}
(4)層次遍歷
即按照層次訪問,通常用佇列來做。訪問根,訪問子女,再訪問子女的子女(越往後的層次越低)(兩個子女的級別相同)
特殊的二叉樹
1.完全二叉樹
CompleteBinaryTree
若設二叉樹的高度為h,除第h層外,其它各層(1~h-1)的結點數都達到最大個數,第h層從右向左連續缺若干結點,這就是完全二叉樹。
2.滿二叉樹
FullBinaryTree
一個高度為h的二叉樹包含正是2^h-1元素稱為滿二叉樹。
6線索二叉樹
編輯
線索二叉樹(保留遍歷時結點在任一序列的前驅和後繼的信息):若結點有左子樹,則其lchild域指示其左孩子,否則令lchild域指示其前驅;若結點有右子樹,則其rchild域指示其右孩子,否則令rchild指示其後繼。還需在結點結構中增加兩個標誌域LTag和RTag。LTag=0時,lchild域指示結點的左孩子,LTag=1時,lchild域指示結點的前驅;RTag=0時,rchild域指示結點的右孩子,RTag=1時,rchild域指示結點的後繼。以這種結點結構構成的二叉線索鍊表,鍊表作為二叉樹的存儲結構,叫做其中指向結點前驅和後繼的指針叫做線索,加上線索的二叉樹稱為線索二叉樹。對二叉樹以某種次序遍歷使其變為線索二叉樹的過程叫做線索化。若對二叉樹進行中序遍歷,則所得的線索二叉樹稱為中序線索二叉樹,線索鍊表稱為為中序線索鍊表。線索二叉樹是一種物理結構。
線索二叉樹的存儲結構
線索二叉樹的存儲結構
在中序線索樹找結點後繼的規律是:若其右標誌為1,則右鏈為線索,指示其後繼,否則遍歷其右子樹時訪問的第一個結點(右子樹最左下的結點)為其後繼;找結點前驅的規律是:若其左標誌為1,則左鏈為線索,指示其前驅,否則遍歷左子樹時最後訪問的一個結點(左子樹中最右下的結點)為其前驅。
在後序線索樹中找到結點的後繼分三種情況:
若結點是二叉樹的根,則其後繼為空;若結點是其雙親的右孩子,或是其雙親的左孩子且其雙親沒有右子樹,則其後繼即為雙親結點;若結點是其雙親的左孩子,且其雙親有右子樹,則其後繼為雙親右子樹上按後序遍歷列出的第一個結點。
數據結構定義為:
1
2
3
4
5
6
7
/*二叉線索存儲表示*/
typedefenum{Link,Thread}PointerTag;/*Link(0):指針,Thread(1):線索*/
typedefstructBiThrNode
{TElemTypedata;
structBiThrNode*lchild,*rchild;/*左右孩子指針*/
PointerTagLTag,RTag;/*左右標誌*/
}BiThrNode,*BiThrTree;
線索二叉樹
線索二叉樹(保留遍歷時結點在任一序列的前驅和後繼的信息):若結點有左子樹,則其lchild域指示其左孩子,否則令lchild域指示其前驅;若結點有右子樹,則其rchild域指示其右孩子,否則令rchild指示其後繼。還需在結點結構中增加兩個標誌域LTag和RTag。LTag=0時,lchild域指示結點的左孩子,LTag=1時,lchild域指示結點的前驅;RTag=0時,rchild域指示結點的右孩子,RTag=1時,rchild域指示結點的後繼。以這種結點結構構成的二叉線索鍊表,鍊表作為二叉樹的存儲結構,叫做其中指向結點前驅和後繼的指針叫做線索,加上線索的二叉樹稱為線索二叉樹。對二叉樹以某種次序遍歷使其變為線索二叉樹的過程叫做線索化。若對二叉樹進行中序遍歷,則所得的線索二叉樹稱為中序線索二叉樹,線索鍊表稱為為中序線索鍊表。線索二叉樹是一種物理結構。
線索二叉樹的存儲結構
線索二叉樹的存儲結構
在中序線索樹找結點後繼的規律是:若其右標誌為1,則右鏈為線索,指示其後繼,否則遍歷其右子樹時訪問的第一個結點(右子樹最左下的結點)為其後繼;找結點前驅的規律是:若其左標誌為1,則左鏈為線索,指示其前驅,否則遍歷左子樹時最後訪問的一個結點(左子樹中最右下的結點)為其前驅。
在後序線索樹中找到結點的後繼分三種情況:
若結點是二叉樹的根,則其後繼為空;若結點是其雙親的右孩子,或是其雙親的左孩子且其雙親沒有右子樹,則其後繼即為雙親結點;若結點是其雙親的左孩子,且其雙親有右子樹,則其後繼為雙親右子樹上按後序遍歷列出的第一個結點。
數據結構定義為:
1
2
3
4
5
6
7
/*二叉線索存儲表示*/
typedefenum{Link,Thread}PointerTag;/*Link(0):指針,Thread(1):線索*/
typedefstructBiThrNode
{TElemTypedata;
structBiThrNode*lchild,*rchild;/*左右孩子指針*/
PointerTagLTag,RTag;/*左右標誌*/
}BiThrNode,*BiThrTree;