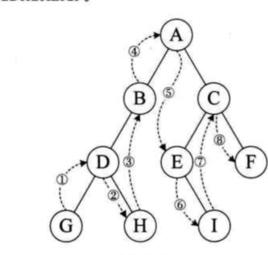
概念含義
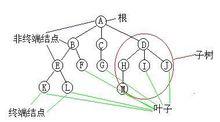 葉子結點
葉子結點葉子結點 就是度為0的結點 就是沒有子結點的結點
n:度為0的結點數,n:度為1的結點 n:度為2的結點數。 N是總結點
在二叉樹中:
n=n+1;
N=n+n+n
例題
一棵樹度為4,其中度為1,2,3,4的結點個數分別為4,2,1,1,則這棵樹的葉子節點個數為多少?
解:因為任一棵樹中,結點總數=度數*該度數對應的結點數+1,所以:
n0+4+2+1+1 = (0*n0 + 1*4 + 2*2 + 3*1 + 4*1)+1
則:n0=8
其中:n0表示葉子結點。
計算方式
該算法的遞歸形式比較容易實現。
具體的代碼塊如下:
int leaf(BiTree root)
{
static int leaf_count = 0; --->在遞歸調用時只進行一次初始化。
if (NULL != root) {
leaf(root->lchild);
leaf(root->rchild);
if (root->lchild == NULL
&& root->rchild == NULL)
leaf_count++;
}
return leaf_count;
}
1,該算法的代碼模組的獨立性算是設計的比較好的。
1.1,耦合比較低,傳入樹的樹根,返回樹的葉子節點的個數。
1.2,內聚比較高,模組中的代碼比較緊密。容易閱讀,易維護。
2,該算法是用遞歸實現的,效率肯定不是很高。
3,該算法是在對樹的後序遍歷的基礎上實現的。如果該節點的左子樹,再右子樹,
最後是根節點。